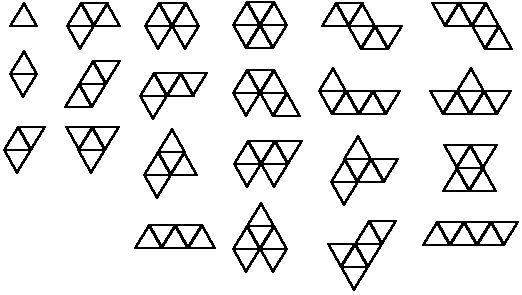
[Home] [Contents] [Figures] [Search] [Help]
[Next Page] [Prev Page] [ Next Chapter] [Prev Chapter]
Fig. 24 illustrates all the different ways of joining triangles through size-six. Note that mirror images are not counted as separate pieces, since it is assumed these are real physical pieces that can be flipped over. These pieces are sometimes referred to as polyiamonds. The numbers of pieces are summarized in Table 1.
Fig. 24
Table 1
The next step is to consider what simple geometrical shapes these pieces might be assembled into. For the triangle, the most obvious patterns are triangular and hexagonal. These are shown in Fig. 25 in increasing size.
Fig. 25
Comparing the numbers in Table 1 with the total numbers of blocks in different-sized sets, we note that none of them match. At this point there are two different schools of thought. Those whose interest is primarily mathematical analysis like to work with complete sets of things, so they would probably either tinker with the definitions of the sets in an attempt to make the numbers match or perhaps abandon this particular line of inquiry. From the practical point of view, on the other hand, there is no good reason why the pieces of a puzzle must comprise a complete mathematical set in order to be interesting. The tabulation of complete sets is useful in that it shows all the pieces that are available without duplication. Example: select a set of nine six-block pieces that assembles into a size-54 hexagon. Second problem: does such a set exist having a unique solution? (Answer unknown).
For those who do insist on working with "complete" mathematical sets, not that of the 12 pieces of size-six, nine of them can be made by joining three two-block rhombuses together all possible ways, as shown in Fig. 26. Of course, this also has practical woodworking significance. Assemble these nine pieces into a 54-block hexagon.
Fig. 26
Now see if the same can be done with another set of nine pieces coincidentally formed by joining two three-block trapezoids all possible ways.
Note also that the entire set of twelve size-six pieces might be assemblable into a 72-block rhombus or rhomboid many different ways. Which of those shown in Fig. 27 are possible to assemble?
Fig. 27
For more information on amusements of this sort, see Martin Gardner's Sixth Book of Mathematical Games from Scientific American.
| ©1990-2005 by Stewart T. Coffin For questions or comments regarding this site, contact the chief metagrobologist: |
[Next Page] [Prev Page] [ Next Chapter] [Prev Chapter]