[Home] [Contents] [Figures] [Search] [Help]
[Next Page] [Prev Page] [ Next Chapter] [Prev Chapter]
Closely related to the polycube puzzles are the so-called packing problems using rectangular blocks. Again many of these are of interest primarily to mathematical analysts, but some of them also make satisfactory assembly puzzles. Take for example the Slothouber-Graatsma Puzzle, which calls for three 1 x 1 x 1 cubes and six 1 x 2 x 2 blocks to be packed into a 3 x 3 x 3 box. There is only one solution. Another is known as Conway's Puzzle after its inventor, mathematician John Conway. It calls for packing three 1 x 1 x 3 blocks, one 1 x 2 x 2 block, one 2 x 2 x 2 block, and thirteen 1 x 2 x 4 blocks into a 5 x 5 x 5 box. It is quite difficult unless one happens to be an expert in this particular branch of mathematics.
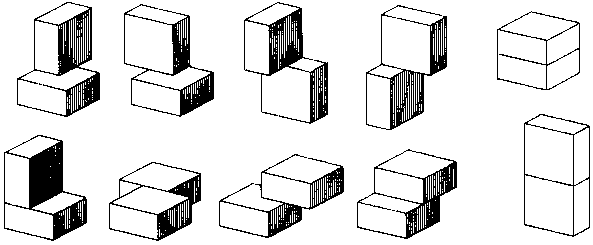
An interesting puzzle is suggested by joining 1 x 2 x 2 blocks in pairs all possible ways. The resulting 10 pieces are shown in Fig. 60. They can be assembled into a 4 x 4 x 5 solid, and there are said to be 25 solutions. Now eliminate the two pieces that are themselves rectangular, and see if the remaining eight (shaded) will assemble into a 4 x 4 x 4 cube. After you have become convinced that they will not, find a set that will by duplicating one piece and eliminating one piece, and note the interesting pattern of symmetry in the solution.
In the same vein, a simple puzzle project is to find all the ways that 1 x 1 x 2 blocks can be joined in pairs. Then assemble them into a rectangular solid and discover one solution having a pattern of reflexive symmetry
Editor's Note: Stewart named this puzzle Patio Block.

Fig. 60
| ©1990-2005 by Stewart T. Coffin For questions or comments regarding this site, contact the chief metagrobologist: |
[Next Page] [Prev Page] [ Next Chapter] [Prev Chapter]