[Home] [Contents] [Figures] [Search] [Help]
[Next Page] [Prev Page] [ Next Chapter] [Prev Chapter]
The term isometric symmetry was introduced without explaining what it meant. A three-dimensional object is said to have isometric symmetry if it has identical non-coplanar axes of symmetry. In other words, it exists in a sort of geometrical vertigo, with no identifiable upright orientation, no top or bottom, front or back, left or right, all being the same. All of the Platonic solids have this property, including their various truncated and stellated variants. Rectangular solids (except the cube) and pyramids (except the tetrahedron) do not have it. The three-dimensional object in question can be anything from a polyhedral solid to a cluster of solids, a nesting of sticks, or whatever.
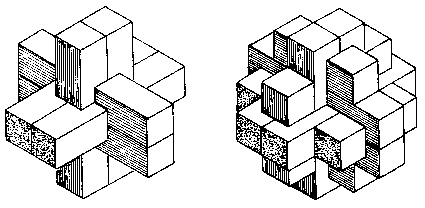
There is another sort of symmetry that most of the burr puzzles in this book have, sometimes referred to as homogeneity or congruence. It is illustrated by the two drawings in Fig. 72. On the left is the standard six-piece burr. The 12-piece burr on the right is representative of a popular family of puzzles, sometimes called pagodas. which lack homogeneity because not only are the sticks of various lengths but also their relative positions are distinguishable.
Fig. 72
The term homogeneous isometric symmetry is so awkward that it will not be used throughout this book, but rather will be implied. Most well-conceived burr puzzles have it, and the lacking of it must be considered an aesthetic blemish. Like so many aesthetic considerations, this one too is rooted firmly in practicality. Most interlocking puzzles have a key piece or sliding axis that constitutes the first step of disassembly. In a symmetrical burr, all pieces have equal standing and are indistinguishable from one another when assembled, thus coyly hiding their identity beneath a geometrical masquerade.
A distinction is made between apparent symmetry and total symmetry. When a puzzle has apparent symmetry, as do practically all well-designed geometrical puzzles, the assembled external shape is symmetrical but not necessarily the insides. When a puzzle has total symmetry, all of the internal surfaces of dissection are symmetrical as well. Such puzzles necessarily have all pieces identical, limiting their possibilities for combinatorial problems, but there are some intriguing exceptions involving color symmetry.
For both practical and aesthetic reasons, as already discussed, anyone who tinkers with geometrical puzzles usually takes for granted the concept of symmetrical external form and internal dissymmetries without giving it much thought. It is interesting to note that all higher animals also have this property, although the exact reasons for it are not at all obvious. If one's body and brain were entirely bilaterally symmetrical, could one tell the difference between left and right, throw a ball, or use a typewriter? Could one even think, in the usual sense of the term?
| ©1990-2005 by Stewart T. Coffin For questions or comments regarding this site, contact the chief metagrobologist: |
[Next Page] [Prev Page] [ Next Chapter] [Prev Chapter]