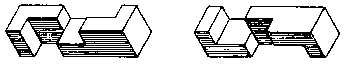
[Home] [Contents] [Figures] [Search] [Help]
[Next Page] [Prev Page] [ Next Chapter] [Prev Chapter]
The interesting variations of this puzzle are quite numerous, and probably others await discovery. In the standard Altekruse Puzzle, each piece has three notches, with the two end notches facing in the same direction. There is a variation in which some pieces have notches facing in opposite directions, and such pieces can be either one of a reflexive pair, as illustrated in Fig. 76. Which combinations using such pieces are possible?
Fig. 76
The repetitive structure of Altekruse pieces can be extended indefinitely to create larger puzzles. Before considering these, note the diminutive version shown in Fig. 77 that uses six pieces of two notches each - three right-handed pieces and three left-handed. Try to solve this puzzle visually, and then discover an interesting variation that does not use equal numbers of right-handed and left-handed pieces (and do not forget that it must be assemblable).
Fig. 77
There is a version that uses 24 sticks, four notches in each, 12 right-handed and 12 left-handed (Fig. 78 on the left). There is a version that uses 36 or 38 identical sticks of five notches each (Fig. 78 on the right), and so on ad infinitum. There are rectangular versions in even greater number. Note that none of these larger versions is homogeneous. Once the basic principle is understood, these larger versions are not very difficult to assemble except that some trial and error may be required to figure out the correct order of assembly. They also require more dexterity of the others, and it helps if the pieces are accurately made.
Fig. 78
Another interesting variation of the Altekruse Puzzle uses pins and holes in place of notches. In its simplest version each piece has one pin and one hole, with six right-handed pieces and six left-handed pieces. An unusual feature of this version is that, with a large supply of pieces to work with, they can be connected end-to-end to make longer sticks and larger, more complex assemblies without limit. To make things more interesting, there need not be equal numbers of the two types of pieces, and there may also be pieces with pins facing in opposite directions. For even more entertainment, add pins or holes in the centers of the pieces (Fig. 79). Just figuring out all the possible pieces is quite a task, and analyzing all of the 12-piece assemblies should keep someone occupied for a long time.
Fig. 79
| ©1990-2005 by Stewart T. Coffin For questions or comments regarding this site, contact the chief metagrobologist: |
[Next Page] [Prev Page] [ Next Chapter] [Prev Chapter]