 |
 |
| Fig. 110 |
[Home] [Contents] [Figures] [Search] [Help]
[Next Page] [Prev Page] [ Next Chapter] [Prev Chapter]
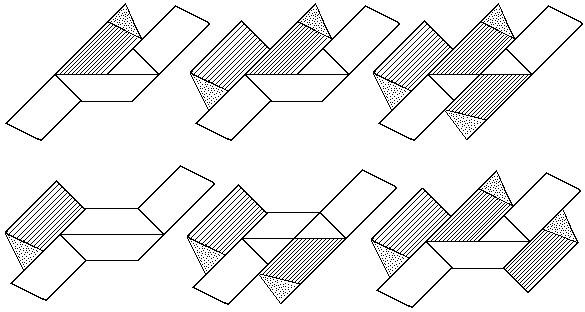
Carrying the development of the Permutated Second Stellation and the Permutated Third Stellation one step further, by lengthening the triangular stick segments even more, one arrives back at an assembly that resembles the nest of twelve triangular sticks shown in Fig. 93, except that now some of them are broken in two internally. The six dissimilar puzzle pieces are shown in Fig. 110. Because of the extra length of the arms, they now interfere with each other during assembly. By an extraordinary coincidence, this results in one of the two solutions being impossible to assemble and three of the four sliding axes being blocked. Thus the puzzle has only one solution and one possible sliding axis of assembly. Consequently it is very difficult.
This remarkable puzzle design has been described as though it were a coincidence of four coincidences. But is it really? The term coincidence would seem to imply chance or luck, whereas this is simply a mathematical reality of the way things are in this world. The only luck involved was that of the person discovering it. Or was it? Perhaps the universe itself is the ultimate example of an improbable coincidence. Why are things as they are?
| ©1990-2005 by Stewart T. Coffin For questions or comments regarding this site, contact the chief metagrobologist: |
[Next Page] [Prev Page] [ Next Chapter] [Prev Chapter]