The Puzzling World of Polyhedral Dissections
By Stewart T. Coffin

[Home] [Contents] [Figures] [Search] [Help]

Chapter 9 - Polyhedral Puzzles with Dissimilar Pieces
Building Blocks

[Next Page] [Prev Page] [ Next Chapter] [Prev Chapter]

In this and the previous two chapters, various polyhedral blocks derived from dissections of the rhombic dodecahedron have been employed for building up puzzle pieces. If the geometry of these pieces is not entirely clear to the reader from the drawings alone, some hands-on experience with the blocks should help to clarify things. If the requirement for accuracy is set aside for the moment, they are all easy to make even with hand tools. This is a good point at which to summarize them.

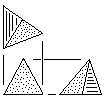
For our purposes, the tetrahedral block is taken as the most basic unit, although of course it could be further subdivided ad infinitum. Since many of the blocks are made equally well from either square or triangular stock, this is conveyed with two sets of drawings in Fig. 112.

		Triangular Stock	Square Stock
T	Tetrahedral Block Basic unit. Made from triangular stock without waste or square stock with waste. See Fig. 90 for more information.
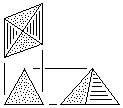
P	Rhombic Pyramid Block Two tetrahedral units. Made from triangular stock without waste or square stock with waste.
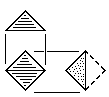
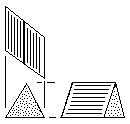
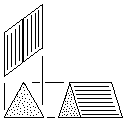
R	Right-Handed Prism Block Three tetrahedral units. Made from either triangular or square stock without waste.
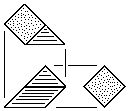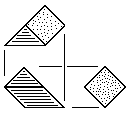
L	Left-Handed Prism Block Three tetrahedral units. Made from either triangular or square stock without waste.
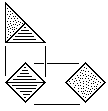
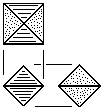
O	Squat Octahedron Block Four tetrahedral units. Made from square stock with waste. Also made of two rhombic pyramid blocks.
C	Six-Sided Center Block Six tetrahedral units. Made from square stock without waste. Also made of two prism blocks. See Fig. 90 for more information.

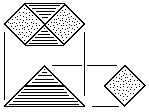Fig. 112

For further clarification, Fig. 113 shows rhombic dodecahedra dissected into these various shapes. The rhombic dodecahedron itself is used as a basic building block in Chapter 8.

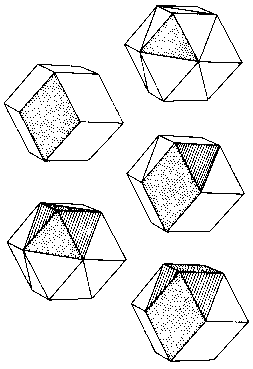
Fig. 113

With only these six building blocks, the number of simple ways in which they can be combined into interlocking puzzles is phenomenal. Just a few more examples will be shown in this chapter.

©1990-2005 by Stewart T. Coffin For questions or comments regarding this site, contact the chief metagrobologist:

[Next Page] [Prev Page] [ Next Chapter] [Prev Chapter]