[Home] [Contents] [Figures] [Search] [Help]
[Next Page] [Prev Page] [ Next Chapter] [Prev Chapter]
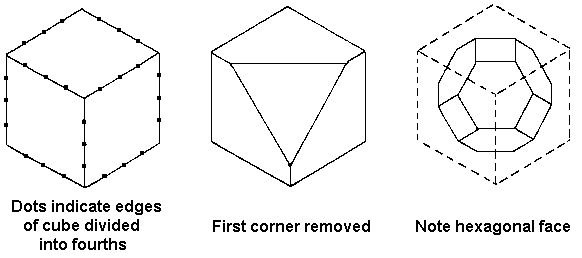
Besides the cube, there are only two other space-filling polyhedra that would appear to have much practical use as puzzle building blocks. One of these is the truncated octahedron. The blocks are fairly easy to make by starting with large wooden cubes and sawing off the eight corners using a suitable jig to hold them accurately (and safely!) in the saw (see Fig. 164). To check for accuracy, the eight new faces should be regular hexagons.
Fig. 164
There are two ways that two such blocks can be joined and six ways that three can be joined, as shown in Fig. 165. These puzzle pieces tend to be anything but interlocking, so most practical puzzle constructions using them are either pyramidal piles or are packed inside a box.
Fig. 165
The set of five pieces shown in Fig. 166 consists of two blocks joined by their square faces plus the four non-straight three-block pieces. They pack into the square box 11 different ways and make a square pyramid three different ways. Note that in the model shown the recessed bottom of the inverted box serves as a convenient base for the square pyramid. The instruction booklet that came with a commercial version of this puzzle showed 15 other symmetrical constructions using some or all of the pieces. How many can the reader discover?

Fig. 166
| ©1990-2005 by Stewart T. Coffin For questions or comments regarding this site, contact the chief metagrobologist: |
[Next Page] [Prev Page] [ Next Chapter] [Prev Chapter]