[Home] [Contents] [Figures] [Search] [Help]
[Next Page] [Prev Page] [ Next Chapter] [Prev Chapter]
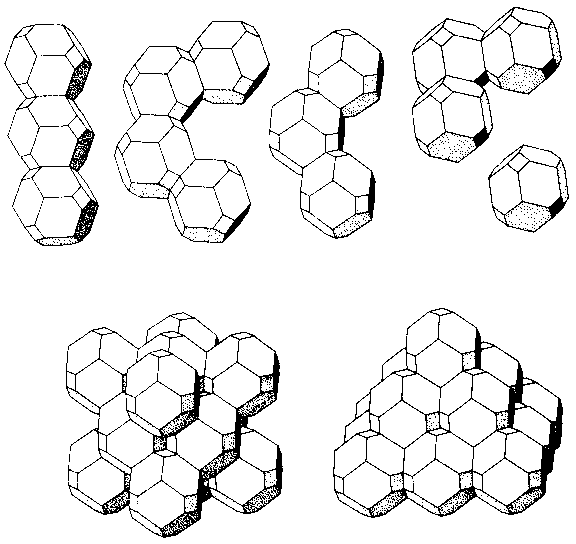
Polyhedral puzzles that are non-interlocking are usually more satisfactory if contained inside a box of some sort. Unlike cubes or even truncated octahedra, rhombic dodecahedra do not rest comfortably in square boxes. This can be corrected somewhat by truncating the R-D blocks. Shown in Fig. 169 is a simple but entertaining puzzle made up of 14 truncated R-D blocks joined together to make five puzzle pieces. They will construct a square pyramidal pile and also a rectangular pyramidal pile. With one piece omitted, they will construct a tetrahedral shape that, surprisingly, fits neatly inside a box. All five pieces pack neatly inside a cubic box, as shown. But the most entertaining trick they do is pack snugly into the box apparently with no vacancy, but with the single block left out!
Fig. 169
The easiest way to make truncated rhombic dodecahedra is to start with large cubic blocks and bevel all the edges at 45 degrees to any desired but uniform depth. With a shallow bevel, the mating surfaces will be small and the glue joints less strong, so it may be desirable to strengthen them by inserting dowels.
Editor's Note: This puzzle has also been called Pyracube.
| ©1990-2005 by Stewart T. Coffin For questions or comments regarding this site, contact the chief metagrobologist: |
[Next Page] [Prev Page] [ Next Chapter] [Prev Chapter]