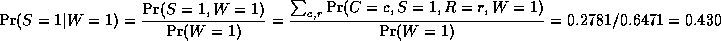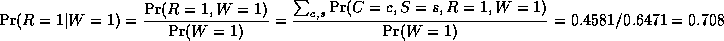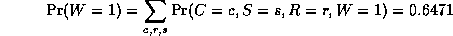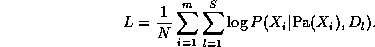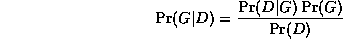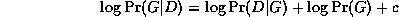A Brief Introduction to Graphical Models and Bayesian Networks

By Kevin Murphy, 1998.

"Graphical models are a marriage between probability theory and graph theory. They provide a natural tool for dealing with two problems that occur throughout applied mathematics and engineering -- uncertainty and complexity -- and in particular they are playing an increasingly important role in the design and analysis of machine learning algorithms. Fundamental to the idea of a graphical model is the notion of modularity -- a complex system is built by combining simpler parts. Probability theory provides the glue whereby the parts are combined, ensuring that the system as a whole is consistent, and providing ways to interface models to data. The graph theoretic side of graphical models provides both an intuitively appealing interface by which humans can model highly-interacting sets of variables as well as a data structure that lends itself naturally to the design of efficient general-purpose algorithms.

Many of the classical multivariate probabalistic systems studied in fields such as statistics, systems engineering, information theory, pattern recognition and statistical mechanics are special cases of the general graphical model formalism -- examples include mixture models, factor analysis, hidden Markov models, Kalman filters and Ising models. The graphical model framework provides a way to view all of these systems as instances of a common underlying formalism. This view has many advantages -- in particular, specialized techniques that have been developed in one field can be transferred between research communities and exploited more widely. Moreover, the graphical model formalism provides a natural framework for the design of new systems." --- Michael Jordan, 1998.

This tutorial

We will briefly discuss the following topics.

Note: Dan Hammerstrom has made a pdf version of this web page. I also have a closely related tutorial in postscript or pdf format.

Articles in the popular press

The following articles provide less technical introductions.

Other sources of technical information

Representation

Probabilistic graphical models are graphs in which nodes represent random variables, and the (lack of) arcs represent conditional independence assumptions. Hence they provide a compact representation of joint probability distributions. Undirected graphical models, also called Markov Random Fields (MRFs) or Markov networks, have a simple definition of independence: two (sets of) nodes A and B are conditionally independent given a third set, C, if all paths between the nodes in A and B are separated by a node in C. By contrast, directed graphical models also called Bayesian Networks or Belief Networks (BNs), have a more complicated notion of independence, which takes into account the directionality of the arcs, as we explain below.

Undirected graphical models are more popular with the physics and vision communities, and directed models are more popular with the AI and statistics communities. (It is possible to have a model with both directed and undirected arcs, which is called a chain graph.) For a careful study of the relationship between directed and undirected graphical models, see the books by Pearl88, Whittaker90, and Lauritzen96.

Although directed models have a more complicated notion of independence than undirected models, they do have several advantages. The most important is that one can regard an arc from A to B as indicating that A ``causes'' B. (See the discussion on causality.) This can be used as a guide to construct the graph structure. In addition, directed models can encode deterministic relationships, and are easier to learn (fit to data). In the rest of this tutorial, we will only discuss directed graphical models, i.e., Bayesian networks.

In addition to the graph structure, it is necessary to specify the parameters of the model. For a directed model, we must specify the Conditional Probability Distribution (CPD) at each node. If the variables are discrete, this can be represented as a table (CPT), which lists the probability that the child node takes on each of its different values for each combination of values of its parents. Consider the following example, in which all nodes are binary, i.e., have two possible values, which we will denote by T (true) and F (false).

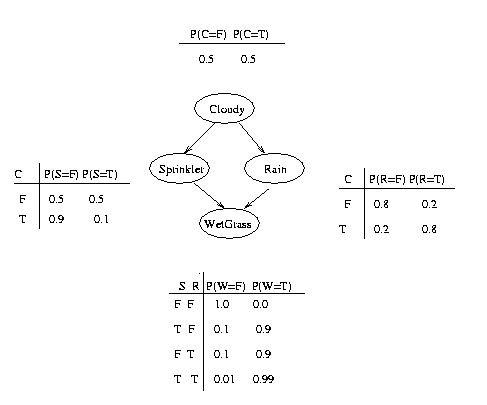
We see that the event "grass is wet" (W=true) has two possible causes: either the water sprinker is on (S=true) or it is raining (R=true). The strength of this relationship is shown in the table. For example, we see that Pr(W=true | S=true, R=false) = 0.9 (second row), and hence, Pr(W=false | S=true, R=false) = 1 - 0.9 = 0.1, since each row must sum to one. Since the C node has no parents, its CPT specifies the prior probability that it is cloudy (in this case, 0.5). (Think of C as representing the season: if it is a cloudy season, it is less likely that the sprinkler is on and more likely that the rain is on.)

The simplest conditional independence relationship encoded in a Bayesian network can be stated as follows: a node is independent of its ancestors given its parents, where the ancestor/parent relationship is with respect to some fixed topological ordering of the nodes.

By the chain rule of probability, the joint probability of all the nodes in the graph above is 

P(C, S, R, W) = P(C) * P(S|C) * P(R|C,S) * P(W|C,S,R)
By using conditional independence relationships, we can rewrite this as 
P(C, S, R, W) = P(C) * P(S|C) * P(R|C)   * P(W|S,R)
where we were allowed to simplify the third term because R is independent of S given its parent C, and the last term because W is independent of C given its parents S and R.

We can see that the conditional independence relationships allow us to represent the joint more compactly. Here the savings are minimal, but in general, if we had n binary nodes, the full joint would require O(2^n) space to represent, but the factored form would require O(n 2^k) space to represent, where k is the maximum fan-in of a node. And fewer parameters makes learning easier.

Are "Bayesian networks" Bayesian?

Despite the name, Bayesian networks do not necessarily imply a commitment to Bayesian statistics. Indeed, it is common to use frequentists methods to estimate the parameters of the CPDs. Rather, they are so called because they use Bayes' rule for probabilistic inference, as we explain below. (The term "directed graphical model" is perhaps more appropriate.) Nevetherless, Bayes nets are a useful representation for hierarchical Bayesian models, which form the foundation of applied Bayesian statistics (see e.g., the BUGS project). In such a model, the parameters are treated like any other random variable, and becomes nodes in the graph.

Inference

The most common task we wish to solve using Bayesian networks is probabilistic inference. For example, consider the water sprinkler network, and suppose we observe the fact that the grass is wet. There are two possible causes for this: either it is raining, or the sprinkler is on. Which is more likely? We can use Bayes' rule to compute the posterior probability of each explanation (where 0==false and 1==true).


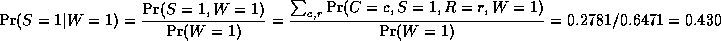
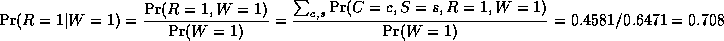
where


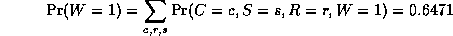
is a normalizing constant, equal to the probability (likelihood) of the data. So we see that it is more likely that the grass is wet because it is raining: the likelihood ratio is 0.7079/0.4298 = 1.647.

Explaining away

In the above example, notice that the two causes "compete" to "explain" the observed data. Hence S and R become conditionally dependent given that their common child, W, is observed, even though they are marginally independent. For example, suppose the grass is wet, but that we also know that it is raining. Then the posterior probability that the sprinkler is on goes down: 
Pr(S=1|W=1,R=1) = 0.1945
This is called "explaining away". In statistics, this is known as Berkson's paradox, or "selection bias". For a dramatic example of this effect, consider a college which admits students who are either brainy or sporty (or both!). Let C denote the event that someone is admitted to college, which is made true if they are either brainy (B) or sporty (S). Suppose in the general population, B and S are independent. We can model our conditional independence assumptions using a graph which is a V structure, with arrows pointing down: 
   B   S
    \ /
     v
     C
Now look at a population of college students (those for which C is observed to be true). It will be found that being brainy makes you less likely to be sporty and vice versa, because either property alone is sufficient to explain the evidence on C (i.e., P(S=1 | C=1, B=1) <= P(S=1 | C=1)). (If you don't believe me, try this little BNT demo!)

Top-down and bottom-up reasoning

In the water sprinkler example, we had evidence of an effect (wet grass), and inferred the most likely cause. This is called diagnostic, or "bottom up", reasoning, since it goes from effects to causes; it is a common task in expert systems. Bayes nets can also be used for causal, or "top down", reasoning. For example, we can compute the probability that the grass will be wet given that it is cloudy. Hence Bayes nets are often called "generative" models, because they specify how causes generate effects.

Causality

One of the most exciting things about Bayes nets is that they can be used to put discussions about causality on a solid mathematical basis. One very interesting question is: can we distinguish causation from mere correlation? The answer is "sometimes", but you need to measure the relationships between at least three variables; the intution is that one of the variables acts as a "virtual control" for the relationship between the other two, so we don't always need to do experiments to infer causality. See the following books for details.

Conditional independence in Bayes Nets

In general, the conditional independence relationships encoded by a Bayes Net are best be explained by means of the "Bayes Ball" algorithm (due to Ross Shachter), which is as follows: Two (sets of) nodes A and B are conditionally independent (d-separated) given a set C if and only if there is no way for a ball to get from A to B in the graph, where the allowable movements of the ball are shown below. Hidden nodes are nodes whose values are not known, and are depicted as unshaded; observed nodes (the ones we condition on) are shaded. The dotted arcs indicate direction of flow of the ball.

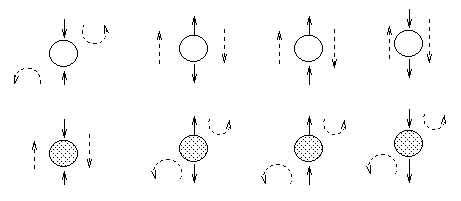
The most interesting case is the first column, when we have two arrows converging on a node X (so X is a "leaf" with two parents). If X is hidden, its parents are marginally independent, and hence the ball does not pass through (the ball being "turned around" is indicated by the curved arrows); but if X is observed, the parents become dependent, and the ball does pass through, because of the explaining away phenomenon. Notice that, if this graph was undirected, the child would always separate the parents; hence when converting a directed graph to an undirected graph, we must add links between "unmarried" parents who share a common child (i.e., "moralize" the graph) to prevent us reading off incorrect independence statements.

Now consider the second column in which we have two diverging arrows from X (so X is a "root"). If X is hidden, the children are dependent, because they have a hidden common cause, so the ball passes through. If X is observed, its children are rendered conditionally independent, so the ball does not pass through. Finally, consider the case in which we have one incoming and outgoing arrow to X. It is intuitive that the nodes upstream and downstream of X are dependent iff X is hidden, because conditioning on a node breaks the graph at that point.

Bayes nets with discrete and continuous nodes

The introductory example used nodes with categorical values and multinomial distributions. It is also possible to create Bayesian networks with continuous valued nodes. The most common distribution for such variables is the Gaussian. For discrete nodes with continuous parents, we can use the logistic/softmax distribution. Using multinomials, conditional Gaussians, and the softmax distribution, we can have a rich toolbox for making complex models. Some examples are shown below. For details, click here. (Circles denote continuous-valued random variables, squares denote discrete rv's, clear means hidden, and shaded means observed.)

For more details, see this excellent paper.

Temporal models

Dynamic Bayesian Networks (DBNs) are directed graphical models of stochastic processes. They generalise hidden Markov models (HMMs) and linear dynamical systems (LDSs) by representing the hidden (and observed) state in terms of state variables, which can have complex interdependencies. The graphical structure provides an easy way to specify these conditional independencies, and hence to provide a compact parameterization of the model.

Note that "temporal Bayesian network" would be a better name than "dynamic Bayesian network", since it is assumed that the model structure does not change, but the term DBN has become entrenched. We also normally assume that the parameters do not change, i.e., the model is time-invariant. However, we can always add extra hidden nodes to represent the current "regime", thereby creating mixtures of models to capture periodic non-stationarities. There are some cases where the size of the state space can change over time, e.g., tracking a variable, but unknown, number of objects. In this case, we need to change the model structure over time.

Hidden Markov Models (HMMs)

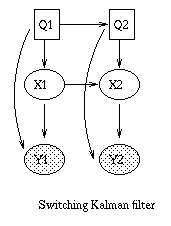
The simplest kind of DBN is a Hidden Markov Model (HMM), which has one discrete hidden node and one discrete or continuous observed node per slice. We illustrate this below. As before, circles denote continuous nodes, squares denote discrete nodes, clear means hidden, shaded means observed.

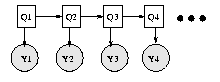
We have "unrolled" the model for 4 "time slices" -- the structure and parameters are assumed to repeat as the model is unrolled further. Hence to specify a DBN, we need to define the intra-slice topology (within a slice), the inter-slice topology (between two slices), as well as the parameters for the first two slices. (Such a two-slice temporal Bayes net is often called a 2TBN.)

Some common variants on HMMs are shown below.

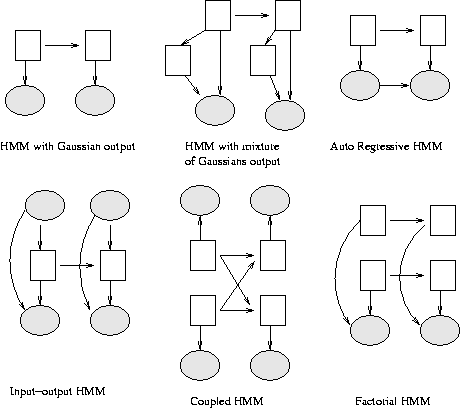
Linear Dynamical Systems (LDSs) and Kalman filters

A Linear Dynamical System (LDS) has the same topology as an HMM, but all the nodes are assumed to have linear-Gaussian distributions, i.e., 
   x(t+1) = A*x(t) + w(t),  w ~ N(0, Q),  x(0) ~ N(init_x, init_V)
   y(t)   = C*x(t) + v(t),  v ~ N(0, R)
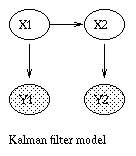
The Kalman filter is a way of doing online filtering in this model. Some simple variants of LDSs are shown below.

The Kalman filter has been proposed as a model for how the brain integrates visual cues over time to infer the state of the world, although the reality is obviously much more complicated. The main point is not that the Kalman filter is the right model, but that the brain is combining bottom up and top down cues. The figure below is from a paper called "A Kalman Filter Model of the Visual Cortex", by P. Rao, Neural Computation 9(4):721--763, 1997.

More complex DBNs

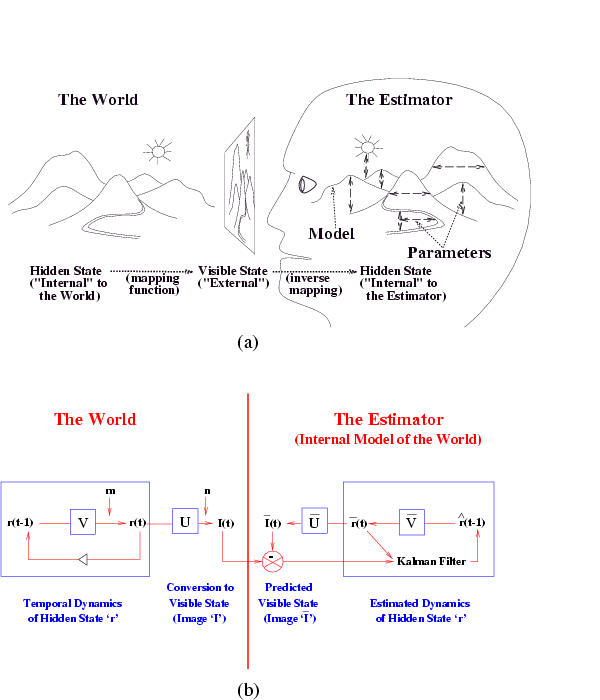It is also possible to create temporal models with much more complicated topologies, such as the Bayesian Automated Taxi (BAT) network shown below. (For simplicity, we only show the observed leaves for slice 2. Thanks to Daphne Koller for providing this figure.)

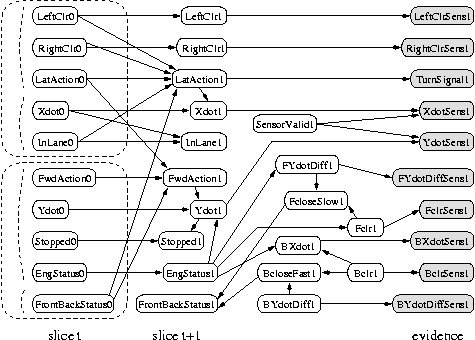
When some of the observed nodes are thought of as inputs (actions), and some as outputs (percepts), the DBN becomes a POMDP. See also the section on decision theory below.

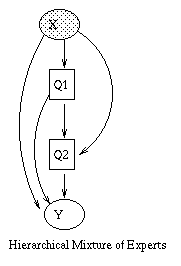
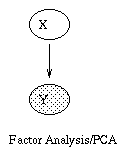
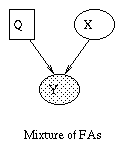
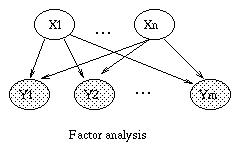
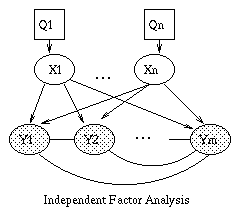
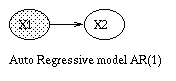
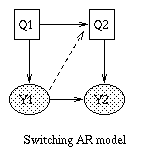
A generative model for generative models

The figure below, produced by Zoubin Ghahramani and Sam Roweis, is a good summary of the relationships between some popular graphical models.

INFERENCE

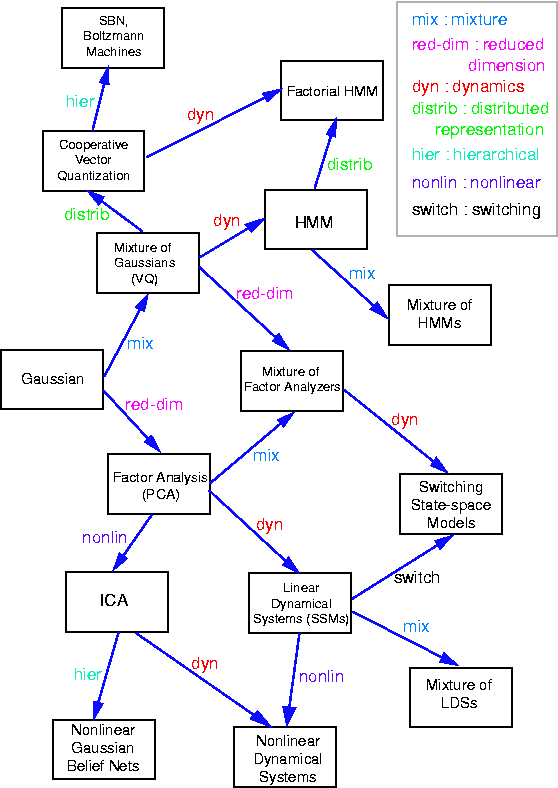
A graphical model specifies a complete joint probability distribution (JPD) over all the variables. Given the JPD, we can answer all possible inference queries by marginalization (summing out over irrelevant variables), as illustrated in the introduction. However, the JPD has size O(2^n), where n is the number of nodes, and we have assumed each node can have 2 states. Hence summing over the JPD takes exponential time. We now discuss more efficient methods.

Variable elimination

For a directed graphical model (Bayes net), we can sometimes use the factored representation of the JPD to do marginalisation efficiently. The key idea is to "push sums in" as far as possible when summing (marginalizing) out irrelevant terms, e.g., for the water sprinkler network

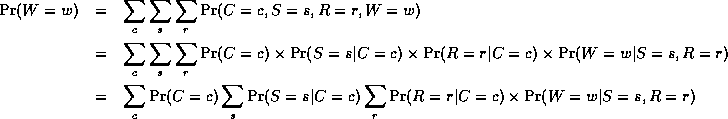
Notice that, as we perform the innermost sums, we create new terms, which need to be summed over in turn e.g.,

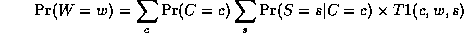
where

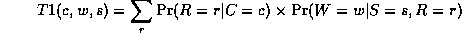
Continuing in this way,

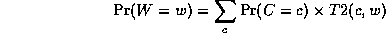
where

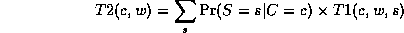
This algorithm is called Variable Elimination. The principle of distributing sums over products can be generalized greatly to apply to any commutative semiring. This forms the basis of many common algorithms, such as Viterbi decoding and the Fast Fourier Transform. For details, see

The amount of work we perform when computing a marginal is bounded by the size of the largest term that we encounter. Choosing a summation (elimination) ordering to minimize this is NP-hard, although greedy algorithms work well in practice.

Dynamic programming

If we wish to compute several marginals at the same time, we can use Dynamic Programming (DP) to avoid the redundant computation that would be involved if we used variable elimination repeatedly. If the underlying undirected graph of the BN is acyclic (i.e., a tree), we can use a local message passing algorithm due to Pearl. This is a generalization of the well-known forwards-backwards algorithm for HMMs (chains). For details, see

If the BN has undirected cycles (as in the water sprinkler example), local message passing algorithms run the risk of double counting. e.g., the information from S and R flowing into W is not independent, because it came from a common cause, C. The most common approach is therefore to convert the BN into a tree, by clustering nodes together, to form what is called a junction tree, and then running a local message passing algorithm on this tree. The message passing scheme could be Pearl's algorithm, but it is more common to use a variant designed for undirected models. For more details, click here

The running time of the DP algorithms is exponential in the size of the largest cluster (these clusters correspond to the intermediate terms created by variable elimination). This size is called the induced width of the graph. Minimizing this is NP-hard.

Approximation algorithms

Many models of interest, such as those with repetitive structure, as in multivariate time-series or image analysis, have large induced width, which makes exact inference very slow. We must therefore resort to approximation techniques. Unfortunately, approximate inference is #P-hard, but we can nonetheless come up with approximations which often work well in practice. Below is a list of the major techniques. Approximate inference is a huge topic: see the references for more details.

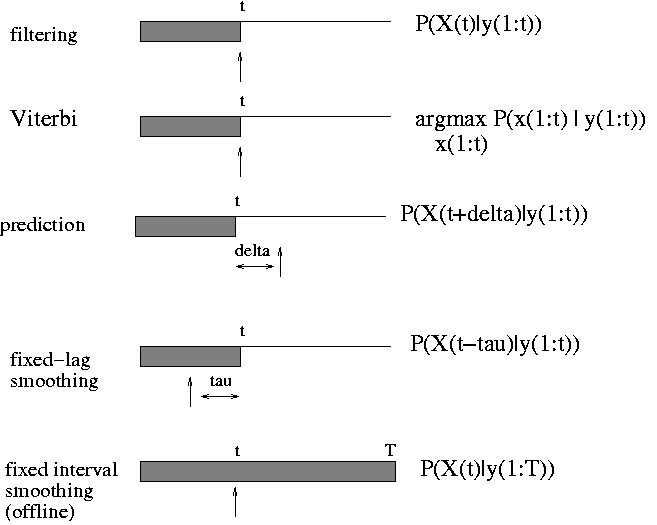
Inference in DBNs

The general inference problem for DBNs is to compute P(X(i,t0) | y(:, t1:t2)), where X(i,t) represents the i'th hidden variable at time and t Y(:,t1:t2) represents all the evidence between times t1 and t2. (In fact, we often also want to compute joint distributions of variables over one or more time slcies.) There are several special cases of interest, illustrated below. The arrow indicates t0: it is X(t0) that we are trying to estimate. The shaded region denotes t1:t2, the available data.

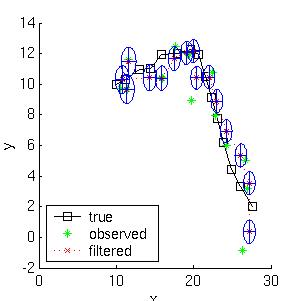
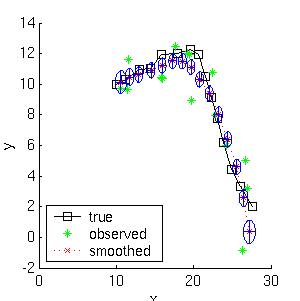
Here is a simple example of inference in an LDS. Consider a particle moving in the plane at constant velocity subject to random perturbations in its trajectory. The new position (x1, x2) is the old position plus the velocity (dx1, dx2) plus noise w. 

[ x1(t)  ] =  [1 0 1 0] [ x1(t-1)  ] + [ wx1  ]
[ x2(t)  ]    [0 1 0 1] [ x2(t-1)  ]   [ wx2  ]
[ dx1(t) ]    [0 0 1 0] [ dx1(t-1) ]   [ wdx1 ]
[ dx2(t) ]    [0 0 0 1] [ dx2(t-1) ]   [ wdx2 ]
We assume we only observe the position of the particle. 
[ y1(t) ] =  [1 0 0 0] [ x1(t)  ] + [ vx1 ]
[ y2(t) ]    [0 1 0 0] [ x2(t)  ]   [ vx2 ]
                       [ dx1(t) ] 
                       [ dx2(t) ]
Suppose we start out at position (10,10) moving to the right with velocity (1,0). We sampled a random trajectory of length 15. Below we show the filtered and smoothed trajectories.
The mean squared error of the filtered estimate is 4.9; for the smoothed estimate it is 3.2. Not only is the smoothed estimate better, but we know that it is better, as illustrated by the smaller uncertainty ellipses; this can help in e.g., data association problems. Note how the smoothed ellipses are larger at the ends, because these points have seen less data. Also, note how rapidly the filtered ellipses reach their steady-state (Ricatti) values. (See my Kalman filter toolbox for more details.)

LEARNING

One needs to specify two things to describe a BN: the graph topology (structure) and the parameters of each CPD. It is possible to learn both of these from data. However, learning structure is much harder than learning parameters. Also, learning when some of the nodes are hidden, or we have missing data, is much harder than when everything is observed. This gives rise to 4 cases: 
Structure   Observability    Method
---------------------------------------------
Known       Full             Maximum Likelihood Estimation
Known       Partial          EM (or gradient ascent)
Unknown     Full             Search through model space 
Unknown     Partial          EM + search through model space

Known structure, full observability

We assume that the goal of learning in this case is to find the values of the parameters of each CPD which maximizes the likelihood of the training data, which contains N cases (assumed to be independent). The normalized log-likelihood of the training set D is a sum of terms, one for each node:
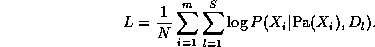We see that the log-likelihood scoring function decomposes according to the structure of the graph, and hence we can maximize the contribution to the log-likelihood of each node independently (assuming the parameters in each node are independent of the other nodes).

Consider estimating the Conditional Probability Table for the W node. If we have a set of training data, we can just count the number of times the grass is wet when it is raining and the sprinler is on, N(W=1,S=1,R=1), the number of times the grass is wet when it is raining and the sprinkler is off, N(W=1,S=0,R=1), etc. Given these counts (which are the sufficient statistics), we can find the Maximum Likelihood Estimate of the CPT as follows:

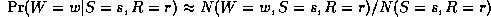
where the denominator is N(S=s,R=r) = N(W=0,S=s,R=r) + N(W=1,S=s,R=r). Thus "learning" just amounts to counting (in the case of multinomial distributions). For Gaussian nodes, we can compute the sample mean and variance, and use linear regression to estimate the weight matrix. For other kinds of distributions, more complex procedures are necessary.

As is well known from the HMM literature, ML estimates of CPTs are prone to sparse data problems, which can be solved by using (mixtures of) Dirichlet priors (pseudo counts). This results in a Maximum A Posteriori (MAP) estimate. For Gaussians, we can use a Wishart prior, etc.

Known structure, partial observability

When some of the nodes are hidden, we can use the EM (Expectation Maximization) algorithm to find a (locally) optimal Maximum Likelihood Estimate of the parameters. The basic idea behind EM is that, if we knew the values of all the nodes, learning (the M step) would be easy, as we saw above. So in the E step, we compute the expected values of all the nodes using an inference algorithm, and then treat these expected values as though they were observed (distributions). For example, in the case of the W node, we replace the observed counts of the events with the number of times we expect to see each event: 
P(W=w|S=s,R=r) = E N(W=w,S=s,R=r) / E N(S=s,R=r)

where E N(x) is the expected number of times event x occurs in the whole training set, given the current guess of the parameters. These expected counts can be computed as follows 

E N(.) = E sum_k I(. | D(k)) = sum_k P(. | D(k))

where I(x | D(k)) is an indicator function which is 1 if event x occurs in training case k, and 0 otherwise.

Given the expected counts, we maximize the parameters, and then recompute the expected counts, etc. This iterative procedure is guaranteed to converge to a local maximum of the likelihood surface. It is also possible to do gradient ascent on the likelihood surface (the gradient expression also involves the expected counts), but EM is usually faster (since it uses the natural gradient) and simpler (since it has no step size parameter and takes care of parameter constraints (e.g., the "rows" of the CPT having to sum to one) automatically). In any case, we see than when nodes are hidden, inference becomes a subroutine which is called by the learning procedure; hence fast inference algorithms are crucial.

Unknown structure, full observability

We start by discussing the scoring function which we use to select models; we then discuss algorithms which attempt to optimize this function over the space of models, and finally examine their computational and sample complexity.

The objective function used for model selection

The maximum likelihood model will be a complete graph, since this has the largest number of parameters, and hence can fit the data the best. A well-principled way to avoid this kind of over-fitting is to put a prior on models, specifying that we prefer sparse models. Then, by Bayes' rule, the MAP model is the one that maximizes
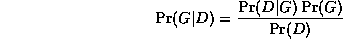Taking logs, we find
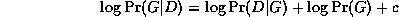where c = - \log \Pr(D) is a constant independent of G.

The effect of the structure prior P(G) is equivalent to penalizing overly complex models. However, this is not strictly necessary, since the marginal likelihood term 

P(D|G) = \int_{\theta} P(D|G, \theta)
has a similar effect of penalizing models with too many parameters (this is known as Occam's razor).

Search algorithms for finding the best model

The goal of structure learning is to learn a dag (directed acyclic graph) that best explains the data. This is an NP-hard problem, since the number of dag's on N variables is super-exponential in N. (There is no closed form formula for this, but to give you an idea, there are 543 dags on 4 nodes, and O(10^18) dags on 10 nodes.)

If we know the ordering of the nodes, life becomes much simpler, since we can learn the parent set for each node independently (since the score is decomposable), and we don't need to worry about acyclicity constraints. For each node, there at most 

\sum_{k=0}^n \choice{n}{k} = 2^n
sets of possible parents for each node, which can be arranged in a lattice as shown below for n=4. The problem is to find the highest scoring point in this lattice.

There are three obvious ways to search this graph: bottom up, top down, or middle out. In the bottom up approach, we start at the bottom of the lattice, and evaluate the score at all points in each successive level. We must decide whether the gains in score produced by a larger parent set is ``worth it''. The standard approach in the reconstructibility analysis (RA) community uses the fact that \chi^2(X,Y) \approx I(X,Y) N \ln(4), where N is the number of samples and I(X,Y) is the mutual information (MI) between X and Y. Hence we can use a \chi^2 test to decide whether an increase in the MI score is statistically significant. (This also gives us some kind of confidence measure on the connections that we learn.) Alternatively, we can use a BIC score.

Of course, if we do not know if we have achieved the maximum possible score, we do not know when to stop searching, and hence we must evaluate all points in the lattice (although we can obviously use branch-and-bound). For large n, this is computationally infeasible, so a common approach is to only search up until level K (i.e., assume a bound on the maximum number of parents of each node), which takes O(n ^ K) time.

The obvious way to avoid the exponential cost (and the need for a bound, K) is to use heuristics to avoid examining all possible subsets. (In fact, we must use heuristics of some kind, since the problem of learning optimal structure is NP-hard \cite{Chickering95}.) One approach in the RA framework, called Extended Dependency Analysis (EDA) \cite{Conant88}, is as follows. Start by evaluating all subsets of size up to two, keep all the ones with significant (in the \chi^2 sense) MI with the target node, and take the union of the resulting set as the set of parents.

The disadvantage of this greedy technique is that it will fail to find a set of parents unless some subset of size two has significant MI with the target variable. However, a Monte Carlo simulation in \cite{Conant88} shows that most random relations have this property. In addition, highly interdependent sets of parents (which might fail the pairwise MI test) violate the causal independence assumption, which is necessary to justify the use of noisy-OR and similar CPDs.

An alternative technique, popular in the UAI community, is to start with an initial guess of the model structure (i.e., at a specific point in the lattice), and then perform local search, i.e., evaluate the score of neighboring points in the lattice, and move to the best such point, until we reach a local optimum. We can use multiple restarts to try to find the global optimum, and to learn an ensemble of models. Note that, in the partially observable case, we need to have an initial guess of the model structure in order to estimate the values of the hidden nodes, and hence the (expected) score of each model; starting with the fully disconnected model (i.e., at the bottom of the lattice) would be a bad idea, since it would lead to a poor estimate.

Unknown structure, partial observability

Finally, we come to the hardest case of all, where the structure is unknown and there are hidden variables and/or missing data. In this case, to compute the Bayesian score, we must marginalize out the hidden nodes as well as the parameters. Since this is usually intractable, it is common to usean asymptotic approximation to the posterior called BIC (Bayesian Information Criterion), which is defined as follows: 
\log \Pr(D|G) \approx \log \Pr(D|G, \hat{\Theta}_G) -  \frac{\log N}{2} \#G
where N is the number of samples, \hat{\Theta}_G is the ML estimate of the parameters, and #G is the dimension of the model. (In the fully observable case, the dimension of a model is the number of free parameters. In a model with hidden variables, it might be less than this.) The first term is just the likelihood and the second term is a penalty for model complexity. (The BIC score is identical to the Minimum Description Length (MDL) score.)

Although the BIC score decomposes into a sum of local terms, one per node, local search is still expensive, because we need to run EM at each step to compute \hat{\Theta}. An alternative approach is to do the local search steps inside of the M step of EM - this is called Structureal EM, and provably converges to a local maximum of the BIC score (Friedman, 1997).

Inventing new hidden nodes

So far, structure learning has meant finding the right connectivity between pre-existing nodes. A more interesting problem is inventing hidden nodes on demand. Hidden nodes can make a model much more compact, as we see below.
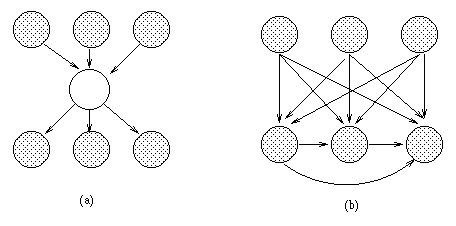(a) A BN with a hidden variable H. (b) The simplest network that can capture the same distribution without using a hidden variable (created using arc reversal and node elimination). If H is binary and the other nodes are trinary, and we assume full CPTs, the first network has 45 independent parameters, and the second has 708.

The standard approach is to keep adding hidden nodes one at a time, to some part of the network (see below), performing structure learning at each step, until the score drops. One problem is choosing the cardinality (number of possible values) for the hidden node, and its type of CPD. Another problem is choosing where to add the new hidden node. There is no point making it a child, since hidden children can always be marginalized away, so we need to find an existing node which needs a new parent, when the current set of possible parents is not adequate.

\cite{Ramachandran98} use the following heuristic for finding nodes which need new parents: they consider a noisy-OR node which is nearly always on, even if its non-leak parents are off, as an indicator that there is a missing parent. Generalizing this technique beyond noisy-ORs is an interesting open problem. One approach might be to examine H(X|Pa(X)): if this is very high, it means the current set of parents are inadequate to ``explain'' the residual entropy; if Pa(X) is the best (in the BIC or \chi^2 sense) set of parents we have been able to find in the current model, it suggests we need to create a new node and add it to Pa(X).

A simple heuristic for inventing hidden nodes in the case of DBNs is to check if the Markov property is being violated for any particular node. If so, it suggests that we need connections to slices further back in time. Equivalently, we can add new lag variables and connect to them.

Of course, interpreting the ``meaning'' of hidden nodes is always tricky, especially since they are often unidentifiable, e.g., we can often switch the interpretation of the true and false states (assuming for simplicity that the hidden node is binary) provided we also permute the parameters appropriately. (Symmetries such as this are one cause of the multiple maxima in the likelihood surface.)

Further reading on learning

The following are good tutorial articles.

Decision Theory

It is often said that "Decision Theory = Probability Theory + Utility Theory". We have outlined above how we can model joint probability distributions in a compact way by using sparse graphs to reflect conditional independence relationships. It is also possible to decompose multi-attribute utility functions in a similar way: we create a node for each term in the sum, which has as parents all the attributes (random variables) on which it depends; typically, the utility node(s) will have action node(s) as parents, since the utility depends both on the state of the world and the action we perform. The resulting graph is called an influence diagram. In principle, we can then use the influence diagram to compute the optimal (sequence of) action(s) to perform so as to maximimize expected utility, although this is computationally intractible for all but the smallest problems.

Classical control theory is mostly concerned with the special case where the graphical model is a Linear Dynamical System and the utility function is negative quadratic loss, e.g., consider a missile tracking an airplane: its goal is to minimize the squared distance between itself and the target. When the utility function and/or the system model becomes more complicated, traditional methods break down, and one has to use reinforcement learning to find the optimal policy (mapping from states to actions).

Applications

The most widely used Bayes Nets are undoubtedly the ones embedded in Microsoft's products, including the Answer Wizard of Office 95, the Office Assistant (the bouncy paperclip guy) of Office 97, and over 30 Technical Support Troubleshooters.

BNs originally arose out of an attempt to add probabilities to expert systems, and this is still the most common use for BNs. A famous example is QMR-DT, a decision-theoretic reformulation of the Quick Medical Reference (QMR) model.

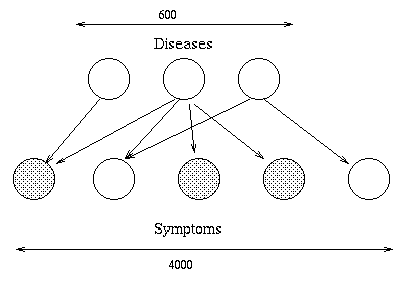Here, the top layer represents hidden disease nodes, and the bottom layer represents observed symptom nodes. The goal is to infer the posterior probability of each disease given all the symptoms (which can be present, absent or unknown). QMR-DT is so densely connected that exact inference is impossible. Various approximation methods have been used, including sampling, variational and loopy belief propagation.

Another interesting fielded application is the Vista system, developed by Eric Horvitz. The Vista system is a decision-theoretic system that has been used at NASA Mission Control Center in Houston for several years. The system uses Bayesian networks to interpret live telemetry and provides advice on the likelihood of alternative failures of the space shuttle's propulsion systems. It also considers time criticality and recommends actions of the highest expected utility. The Vista system also employs decision-theoretic methods for controlling the display of information to dynamically identify the most important information to highlight. Horvitz has gone on to attempt to apply similar technology to Microsoft products, e.g., the Lumiere project.

Special cases of BNs were independently invented by many different communities, for use in e.g., genetics (linkage analysis), speech recognition (HMMs), tracking (Kalman fitering), data compression (density estimation) and coding (turbocodes), etc.

For examples of other applications, see the special issue of Proc. ACM 38(3), 1995, and the Microsoft Decision Theory Group page.

Applications to biology

This is one of the hottest areas. For a review, see

Recommended introductory reading

Books

In reverse chronological order (bold means particularly recommended)

Review articles

Exact Inference

Approximate Inference

Learning

DBNs