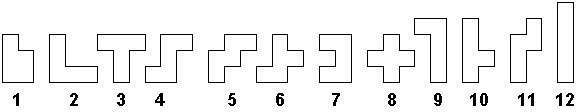
[Home] [Contents] [Figures] [Search] [Help]
[Next Page] [Prev Page] [ Next Chapter] [Prev Chapter]
As already shown, joining five squares together all possible ways produces a set of 12 puzzle pieces. Popularly known as pentominoes (Fig. 31). These occupy much of Golomb's book and have received much attention from others also. The total of 60 blocks is a most fortuitous number because it has so many factors. The earliest reference to a puzzle of this sort appears to be in The Canterbury Puzzles, by Henry Dudeney, published in 1907. The idea is so obvious that it may have to many persons independently.
Fig. 31
The pentominoes are capable of being assembled into four different rectangles - 3 x 20, 4 x 15, 5 x 12, and 6 x 10. The first investigation of these by computer was probably by Dana Scott in 1958. The results were summarized in an article by C. J. Bouwkamp in the Journal of Combinatorial Theory in 1969. There are 2, 368, 1,010, and 2,339 solutions to these four rectangular assemblies. One of each is illustrated in Fig. 32.
Fig. 32
Editor's Note: Click on any of the rectangles to see the solutions computed by a Java applet provided by Gerard Putter of The Netherlands.
With 2,339 solutions, you might expect that placing the 12 pieces onto a 6 x 10 tray should be quite easy. If so, you are due for a surprise! One of the charms of puzzles of this sort is that the first few pieces fall into place and nestle together as though they were made just for each other's company. The next few pieces maybe a bit more troublesome, but they finally settle down happily into place too. It is always the last one or two pieces that are the rascals. As you carefully rearrange things to suit them, then other pieces become the outcasts. Reluctantly you have no choice but to break up combinations that seemed so content together. Alas, you have made the situation worse instead of better, for now there are three that won't go in. In a moment of frustration, you are tempted to brusquely dump the lot out of the tray and start afresh. But no, you take the gentler and wiser approach of patiently switching just a few pieces back and forth, when suddenly the solution reveals itself as the remaining empty space just happens to match the last piece. As it drops snugly into place, there is a sense of resolution and harmony that any sensible person must welcome these days, especially if you have just scanned the headlines of the daily news or perhaps driven through Harvard Square in rush-hour traffic!
Although it was mentioned earlier that crude models will usually suffice for experimental work, that was not necessarily intended as a recommendation. Here is a case where one might well develop a deeper relationship with this captivating set of puzzle pieces by making them accurately and solidly of attractive hardwood, with a smooth finish and close fit and with a matching tray (Fig. 33). They will repay your consideration many times over.
Fig. 33
What may at first seem like a random process of placing the first few pieces on the tray is anything but. Never underestimate the amazing power of the human brain. Which gets even better with practice. For example, you will find some pieces much more cooperative than others. Piece no. 1 is the most tractable. Resist the temptation to place it early - it is your trump and should be kept in reserve until you really need it. Pieces that decline to fit nicely into the corners are the most troublesome. Piece no. 8 is the worst - it refuses altogether. Yet even it has a companion in piece no. 7, so let the pair of them mate. Try to fill the corners first, the ends next, and work toward the center.
For an even more methodical (but less entertaining) approach, consider how a complete analysis of this puzzle might be made. Number the spaces on the 6 x 10 tray 1 to 60 as shown (Fig. 34). Always try to fill the lowest numbered unfilled space with the lowest numbered remaining piece. So, start by placing piece no. 1 on space no. 1. Since this piece has no symmetry, it can be oriented four different ways by rotation plus four more when flipped over, six of which will cover space no. 1. With piece no. 1 in place, try placing piece no. 2 in the next numbered empty space. Piece no. 2 has four orientations by rotation, but because of symmetry it need not be flipped over (likewise pieces no. 3, no. 5, and no. 7). Continue placing pieces in this manner. Note that piece no. 4 has twofold rotational symmetry, so it has only two orientations plus two more when flipped. Piece no. 12 has both rotational and reflexive symmetry, so only two possible orientations. Piece no. 8 is the most symmetrical of all, with only one possible orientation. Furthermore, because of symmetries of the tray, the location of the starting piece can be confined to one quadrant.
 |
|
Fig. 34
Continuing methodically in this manner, one arrives at either a solution or an impasse. When an impasse is reached, the last piece placed is tried in every possible orientation. If that fails, the same is tried with the previously placed piece. Without belaboring all of the details, the point is that by proceeding methodically along these lines, or by some other similar scheme, one eventually tries every piece in every possible location and orientation, and compiles a complete list of solutions (or proves that none exists). If all of this sounds exceedingly arduous, it is indeed, and in the case of this particular example so much so as to be beyond practical human capability. This is where computers come into play. They are perfectly suited for this sort of mindless task. They do in seconds what might take a person days or months, and do so with much less likelihood of error.
| ©1990-2005 by Stewart T. Coffin For questions or comments regarding this site, contact the chief metagrobologist: |
[Next Page] [Prev Page] [ Next Chapter] [Prev Chapter]