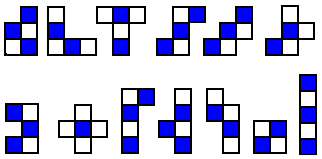
[Home] [Contents] [Figures] [Search] [Help]
[Next Page] [Prev Page] [ Next Chapter] [Prev Chapter]
The joined-square combinatorial puzzles just described bear a close resemblance to the checkerboard dissections discussed in the previous chapter. The distinction between dissection and combinatorial puzzles has little to do with appearance, but rather with method of creation. The classification is not always precise, and the two categories tend to overlap. Consider the checkerboard puzzle shown in Fig 35, which appeared in The Canterbury Puzzles. The pieces are printed on one side only so may not be flipped.
Fig. 35
At first glance, this might appear to be just another checkerboard dissection like those mentioned in the previous chapter. Upon closer scrutiny. However, it is obvious that the pieces were not created by a process of dissection. Rather, Dudeney must have taken the set of 12 pentominoes, added the 2 x 2 square to bring the square count up to 64, assembled all of the pieces into an 8 x 8 square, and lastly added the checkering.
In trying to solve this puzzle, one might start by assuming that Dudeney probably placed the square piece symmetrically in the center for aesthetic reasons. (Before checkering, there are 65 solutions with this arrangement.) With the 2 x 2 checkered square thus centered, by placing the cross piece in each of its four possible locations, one discovers the impossibility of any such solution. This puzzle is known to have four solutions, but all with the square piece off center. Did Dudeney introduce this slight aesthetic anomaly just to confuse us? We will never know for sure but if he did, why then would he have chosen a version with four solutions instead of just one, making it that much easier? A puzzle within a puzzle!
Of all the checkerboard puzzles in Slocum's Compendium, only one is said to be of recent vintage. It may appear at first glance to be just a variation of the Dudeney puzzle. But it was designed by Kathy Jones, which should alert any puzzle connoisseur to expect something thoughtfully conceived and executed. The pieces are checkered on both sides and may or may not be the same on both sides. The puzzle has 1,294 checkered solutions, and the 2 x 2 square can be in any possible position. It also solves several other problems. Three of the solutions with the 2 x 2 square in two different locations are shown in Fig. 36. Note that not quite enough information is given here to determine the exact checkering on both sides of all pieces. The puzzle is produced by Kadon Enterprises, Inc.
Fig. 36
| ©1990-2005 by Stewart T. Coffin For questions or comments regarding this site, contact the chief metagrobologist: |
[Next Page] [Prev Page] [ Next Chapter] [Prev Chapter]