[Home] [Contents] [Figures] [Search] [Help]
[Next Page] [Prev Page] [ Next Chapter] [Prev Chapter]
Solving or attempting to solve a mechanically manipulative puzzle analytically, with all of the action taking place unseen inside a computer, may not sound like much fun except for the computer fanatic. Be that as it may, the computer is now frequently being used as an aid in the design and optimization of combinatorial puzzles. Many examples will be given in this book. One of the more impressive of these is the Cornucopia Puzzle.
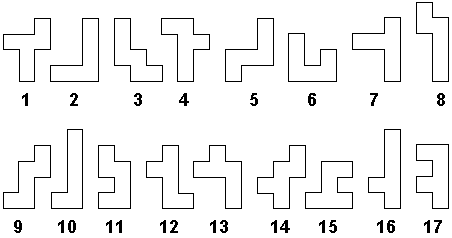
It was shown previously that joining six squares all possible ways produces a set of 35 puzzle pieces. Now, from this set, eliminate all pieces having reflexive or rotational symmetry and all those containing a 2 x 2 square because they are less desirable for various reasons already explained. The remaining 17 pieces are the set of Cornucopia pieces (Fig. 37).

Fig. 37
A subset of any 10 of these pieces will fit onto an 8 x 8 board leaving four empty squares. There are 10 different ways that these four empty squares can be arranged in fourfold symmetry (disregarding reflections) as shown in Fig. 38.
Fig. 38
A subset of 10 Cornucopia pieces can also be assembled to form a solid 6 x 10, 5 x 2, or 4 x 15 rectangle. (Note: the 3 x 20 rectangle is impossible Can the reader discover a neat and simple proof of this? Hint: place piece no. 1, 3, 4, 5, 7, 9, 12, 13, or 15 anywhere in the 3 x 20 rectangle as in Fig. 39 and see what problem then arises.) (Answer)
Fig. 39
Combinatorial theory shows that a subset of 10 pieces can be chosen from a set of 17 pieces 19,448 different ways. Which of these subsets will fit any of the boards shown in Fig. 38, and in how many different ways? Expert puzzle analyst Mike Beeler decided to find the answers to these questions with the aid of a computer. Even with state-of-the-art equipment and clever short cuts, this probably invoked more computation than any previous puzzle analysis and by a wide margin. The final results show 8,203 usable subsets and 105,902 solutions, any one of which constitutes an interesting and challenging puzzle problem, hence the name Cornucopia. This suggested the possibility of producing a series of Cornucopia puzzles whereby each set of pieces would be unique, and each with its own unique solution or solutions. (The idea itself is also believed to be unique!). One hundred such sets were produced in wood in 1985 and are now in the hands of puzzle collectors. The remainder are contained in a stack of papers a foot high!
At the beginning of the Cornucopia project, as the computer started to spew out solutions, we wondered if any subset would be found that made all 13 patterns. Preliminary results indicated this to be very unlikely. To our surprise, however, near the end of the run one prolific subset was discovered that failed to do so by the narrowest margin. It is shown in Fig. 40, with a tabulation of all its copious solutions given in Table 3. To gain some appreciation of the power and speed of a computer, the reader is invited to make this subset of pieces and try to solve just one of the other 56 solutions listed. Now imagine all 57 of them being solved in a few seconds!
Fig. 40 - The Copious Cornucopia
| Pattern | Total Number of Solutions |
|---|---|
| A | 7 (One Shown) |
| B | 1 |
| C | 0 |
| D | 1 |
| E | 11 |
| F | 1 |
| G | 1 |
| H | 1 |
| I | 4 |
| J | 1 |
| 6 X 10 | 15 |
| 5 X 12 | 12 |
| 4 X 15 | 2 |
Table 3
Editor's Note: Click on any of the patterns to see the solutions computed by a Java applet provided by Gerard Putter of The Netherlands.
With polyomino-type puzzles like Cornucopia, when many solutions are known, here is an interesting exercise: display all of them together and have several friends judge which they consider to be the most and least pleasing to the eye. If there is any consistency in the judging, try to determine what characteristics are common to those judged most or least pleasing. Finally, try to define these characteristics mathematically.
After staring at thousands of Cornucopia solutions, the author has selected the two shown in Fig. 41 as being a good pair for illustrating this game. Everyone polled by the author preferred the same one. The other one has at least four easily recognizable and describable flaws. What are they? (Answer) Paradoxically, perhaps the most distinguishing feature of a pleasing polyomino pattern is its lack of any distinguishing features! Evidently the mind's eye prefers randomness in such designs. We all know what randomness is, or think we know until we try to define it mathematically. Randomness is, almost by definition, something that cannot be defined mathematically! And even if the rules for randomness could be stated mathematically, what about the rules for the rules?
Fig. 41
To further compound this strange paradox, at the same time the eye goes to the opposite extreme and automatically takes for granted absolute conformity to the square grid as an unspoken rule. Any deviation from this, as in the example in Fig. 42, cries out as blatantly as would a sour note in a Mozart serenade or an obscenity in an Emily Dickinson poem!
Fig. 42
It is interesting to note that the basic element of a Cornucopia-type puzzle is symmetrical - a square, and the overall assembly is also symmetrical - likewise a square. A dissymmetry occurs between these two extremes in the permutated shape of the puzzle pieces. Thus, the order - symmetry - dissymmetry - symmetry represents in itself another, more abstract sort of symmetry (Fig. 43a).
Fig. 43a
A typical die-cut jigsaw puzzle is an example of a different order of symmetry which is itself non-symmetrical (Fig. 43b).
Fig. 43b
A third order of symmetry would be represented by bathroom tiles on a typical floor (Fig. 43c).
Fig. 43c
Can you discover other orders of symmetry? This term, and in fact the whole concept of order of symmetry, was developed just as a curiosity as this chapter was being cut and pasted for at least the tenth time. This might be an interesting subject of study itself. Practically all puzzles described in this book are inherently of the symmetrical order: symmetry - dissymmetry - symmetry. The intriguing symmetries of the polyhedral shapes are often what attract the attention of the viewing public, much to the chagrin of the designer for all of the creative work lies hidden within and is so often overlooked.
Traditionally, artistic endeavors from music to poetry to oil paintings have nearly always been framed in symmetry of some sort or at least were until this century. Yet symmetry is a hopelessly sterile artistic medium within which to actually work. All creativity involves a judicious departure from symmetry inside this symmetrical framework.
| ©1990-2005 by Stewart T. Coffin For questions or comments regarding this site, contact the chief metagrobologist: |
[Next Page] [Prev Page] [ Next Chapter] [Prev Chapter]