[Home] [Contents] [Figures] [Search] [Help]
[Next Page] [Prev Page] [ Next Chapter] [Prev Chapter]
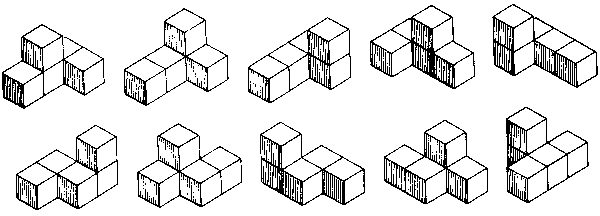
There are 12 pentacubes that are flat (the solid pentominoes) and 17 that are not. There are 12 that have an axis of symmetry and 17 that do not. There are 12 that neither lie flat nor have an axis of symmetry. If we arbitrarily eliminate the two of these that fit inside a 2 x 2 x 2 box, then a set of 10 pieces remains (see Fig. 58).
Fig. 58
According to a computer analysis by Beeler, these pieces pack into a 5 x 5 x 2 box 19,264 different ways, and it is not very difficult to find one of them. To make this puzzle more interesting, the pieces are checkered (Fig. 59). There are two ways that one might go about this. You could randomly checker the pieces and then try to assemble checkered solutions. There are 512 different ways of checkering the pieces, of which 511 have solutions and one does not. So it would be remotely possible, if you were exceedingly unlucky, to end up that way with an impossible puzzle. The better way is to assemble the puzzle first and then add the checkering. This way you are sure of having a solution. Now try to find a second perfectly checkered solution with this set of pieces. Of the 511 ways of checkering the pieces with solutions, 510 of them have multiple solutions and one is a unique solution. So there is this very slight chance that your puzzle may not have a second checkered solution, but you may never know for sure, because finding the other solutions is very difficult (unless you use a computer). How remarkable that out of the 512 possible checkerings, just one should be impossible to assemble checkered and just one other should have a unique solution!
Editor's Note: Stewart named this puzzle Unhappy Childhood.

Fig. 59
| ©1990-2005 by Stewart T. Coffin For questions or comments regarding this site, contact the chief metagrobologist: |
[Next Page] [Prev Page] [ Next Chapter] [Prev Chapter]