[Home] [Contents] [Figures] [Search] [Help]
[Next Page] [Prev Page] [ Next Chapter] [Prev Chapter]
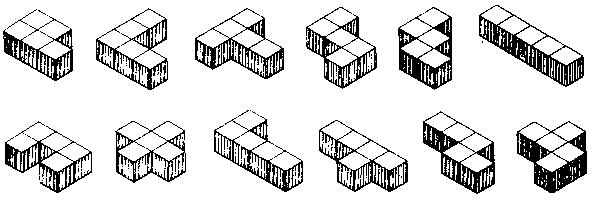
Another popular cubic block puzzle is the set of 12 solid pentominoes. Those are of course the set of pieces made by joining five squares all possible ways, discussed in Chapter 2, except in this case cubic blocks are used in place of squares. The idea of a puzzle set made of such pieces is so obvious that it probably occurred to several persons independently. The earliest references known to the author are associated with Martin Gardner's mathematical recreations column in Scientific American around 1958. They were implied in an article by Golomb in The American Mathematical Monthly, December 1954, and are discussed in his book Polyominoes.
The solid pentominoes (Fig. 56) pack into the following rectangular solids: 2 x 3 x 10, 2 x 5 x 6, and 3 x 4 x 5. Bouwkamp's computer analysis found there to be 12, 264, and 3,940 solutions to these, and these numbers have been confirmed by many other analysts. If you did not learn your lesson with the flat pentominoes, and you think that, with 3,940 solutions, packing these pieces into a 3 x 4 x 5 box ought to be easy, you are in for an even bigger surprise this time!
Fig. 56
The solid pentominoes make a very satisfactory set of puzzle pieces when accurately crafted of nice hardwoods and packaged in a suitable box. Many interesting puzzle problems and pastimes, using either the full set of pieces or subsets, are crammed into Quintillions, a booklet published by Kadon Enterprises. Or you can invent your own puzzle problems.
Fig. 57
| ©1990-2005 by Stewart T. Coffin For questions or comments regarding this site, contact the chief metagrobologist: |
[Next Page] [Prev Page] [ Next Chapter] [Prev Chapter]