[Home] [Contents] [Figures] [Search] [Help]
[Next Page] [Prev Page] [ Next Chapter] [Prev Chapter]
This is an appropriate point at which to digress for a moment and introduce the idea of a difficulty index for a combinatorial puzzle. Puzzles must by definition have some element of difficulty. Making a puzzle more difficult may in some circumstances be an improvement in design, if not carried to extremes and if not to the detriment of other considerations. In any case, some way of predicting the relative difficulty of similar puzzle designs would be a useful tool for the designer.
Consider the solid six-piece burr. Given a drawing of the assembled burr or some familiarity with it, the only real problem is determining the relative location and orientation of the six pieces. Select any one of the six pieces at random for the bottom piece. Usually it is obvious from the notching which side should face the center. Now for the back piece, one has a choice of any of the remaining five, and it can be turned end-for-end, hence a total of ten possibilities. For the next piece, say on the left, there are six choices, and so on. Thus, to make a complete analysis of the puzzle by trying every piece in every position. There are a total of 10 x 8 x 6 x 4 x 2 or 3,840 possibilities to be considered. This number divided by the number of solutions is the difficulty index of that particular design.
The difficulty index of Burr No. 305 is 3,840. While that may seem like a large number of moves, most of them are skipped by using common sense, and so this would be a puzzle of medium difficulty. Identical pairs of pieces, symmetrical pieces, and multiple solutions all decrease the difficulty index. There is one charming type of piece known as an ambiguous piece, because you cannot tell from the notches which side should face the center, and there are different degrees of ambiguity. Piece No. 9 in Fig. 67 is an example of the most ambiguous type because any one of its four sides might face the center. This would increase the difficulty index by an additional factor of four, but because it is also symmetrical the net increase would be a factor of two.
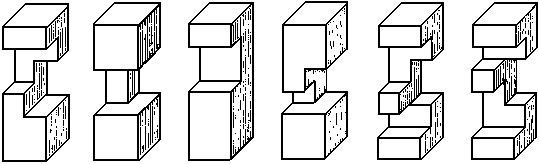
The mischievous role of the ambiguous piece was not taken into account in the analysis that led to the illumination of Burr No. 305. Adding this newfound ingredient to the recipe another delectable puzzle comes to light - Burr No. 306 illustrated in Fig. 69. It uses pieces 6, 9, 12, 21, 22, and 23, and has a difficulty index of 7,680.
Note that a set of seven pieces will allow both Burr No. 305 and Burr No. 306 to be constructed.
Fig. 69
| ©1990-2005 by Stewart T. Coffin For questions or comments regarding this site, contact the chief metagrobologist: |
[Next Page] [Prev Page] [ Next Chapter] [Prev Chapter]