De Jong's test suite

In this section I will present the performance of various optimization algorithms on De Jong's five function test suite. De Jong first suggested this set in his work ``An analysis of the behaviour of a class of genetic adaptive systems'' [De Jong, 1975]. He chose these functions because they represent the common difficulties in optimization problems in an isolated manner. By running the comparisons on these functions, one can make judgments about the strengths and weaknesses of particular algorithms. Also, De Jong's functions are quite popular in genetic algorithms literature, so it is possible to make direct comparisons.

  
Figure: De Jong's functions. The graphs are rotated and modified by order preserving transforms for clarity.

I should emphasize that all these results are only obtained from particular implementations of these algorithms. In particular the GENEsYs package [Bäck and Hoffmeister, 1992] was used for the genetic algorithms, the ASA package [Ingber, 1993] was used for simulated annealing, and the programs from ``Numerical Recipes in C'' [Press et al., 1992] were used for implementations of Powell's method and downhill simplex. Other implementations, or other parameter settings may give different results. Furthermore, the topic of optimization has a vast literature. I discovered that the M.I.T. library has 1240 volumes on the subject, when I tried to do a literature search. Thus it was impossible to run comparison tests with all known methods. Instead I compared my program to a subset of well known, widely used methods.

Figure shows the graphs and equations for the five De Jong functions. Below are their brief descriptions, and the problems they represent:

• SPHERE is the dream of every optimization algorithm. It is smooth, it is unimodal, it is symmetric and it does not have any of the problems we have discussed so far. The performance on SPHERE is a measure of the general efficiency of the algorithm.
• ROSENBROCK is the nightmare. It has a very narrow ridge. The tip of the ridge is very sharp, and it runs around a parabola. Algorithms that are not able to discover good directions underperform in this problem.
• STEP is the representative of the problem of flat surfaces. Flat surfaces are obstacles for optimization algorithms, because they do not give any information as to which direction is favorable. Unless an algorithm has variable step sizes, it can get stuck on one of the flat plateaus.
• QUARTIC is a simple unimodal function padded with noise. The gaussian noise makes sure that the algorithm never gets the same value on the same point. Algorithms that do not do well on this test function will do poorly on noisy data.
• FOXHOLES is an example of many (in this case 25) local optima. Many standard optimization algorithms get stuck in the first peak they find.

Figure gives comparative results of my program to four well known algorithms, the standard genetic algorithm [Holland, 1975], simulated annealing [Kirkpatrick et al., 1983], Powell's method [Powell, 1964], and downhill simplex [Nelder and Mead, 1965].

Note that the standard genetic algorithm is the least efficient of all. It usually does the most number of function evaluations. The numerical algorithms, Powell's method and downhill simplex, do well in terms of efficiency. However they are not robust in the existence of flat surfaces (step function), or local optima (shekel's foxholes). Adaptive simulated annealing is able to solve all the problems consistently, although it is not as efficient as the numerical algorithms. My program, not only finds the global optimum in all five cases, its efficiency is comparable, if not better, than the other ones.

  
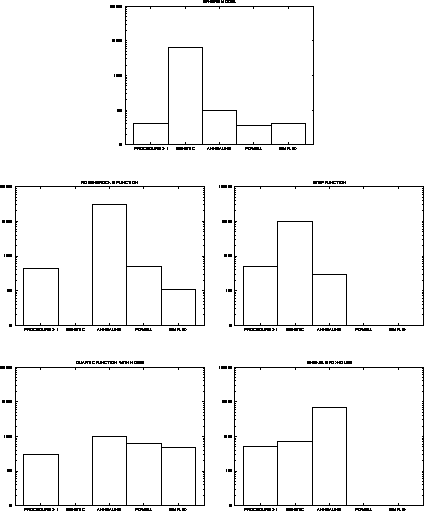
Figure: Comparison of five algorithms on De Jong's functions. The vertical bars represent the number of function evaluations to find the global optimum. The scale is logarithmic and the numbers are averaged over ten runs. No bar was drawn when an algorithm could not find the global optimum consistently.