[Home] [Contents] [Figures] [Search] [Help]
[Next Page] [Prev Page] [ Next Chapter] [Prev Chapter]
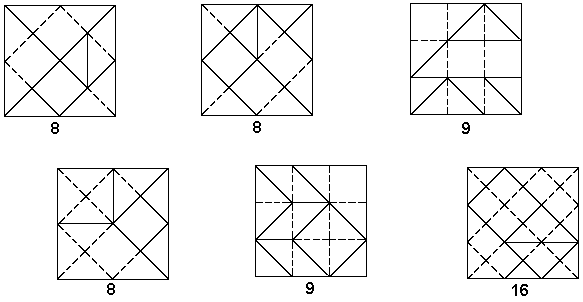
The great popularity of Tangram has spawned many imitations. Most notable of these were the famous Anchor Stone puzzles produced by Richter and Co. of Germany starting in the 1800s and on into the early 1900s. In Puzzles Old and New, Botermans and Slocum show 36 different designs and some of these are worth examining. Six of them, including Tangram, are squares dissected according to the usual square grid with diagonals. Three of these however, are on a grid with a finer scale than Tangram, i.e. containing more grid squares and unit triangles. The diagrams in Fig. 12 should make this clear. The number below each one indicates the number of grid squares enclosed for the coarsest grid that will conform.
Fig. 12
For a given number of pieces, dissections with coarser grids are likely to have more mutually compatible edges - thus the three on the left in Fig. 12 are the better designs in this respect. A dissection that accomplishes its purpose with the fewest pieces is usually to be preferred - thus the two on the left in Fig. 12 emerge as the better designs. The final test is to see which of these two sets constructs more interesting puzzle figures, and this task is left to the reader. The one on the far left is of course Tangram, and the other one was sold under the name Pythagoras.
Incidentally, note that the next smaller possible grid would contain only four squares and eight unit triangles. Are these too few to make an interesting puzzle? The most obvious such set (see Fig. 13) would be Tangram with the two large triangles omitted. This simple little set of five pieces probably contains a treasure-trove of undiscovered recreation: For example, how many convex patterns will it form? (Answer)
Fig. 13
A square can be dissected into numbers of equal isosceles right-angled triangles given by the following series: 2, 4, 8, 16, ... What is the next number in this series? (This question is reminiscent of "IQ" tests school children used to be given, and probably still are. Example: given the series 4, 6, 8, ..., what is the next number? A precocious student interested in prime numbers might answer 9, while one intrigued by the Platonic solids might say 12. But of course, by the time the students are supposed to know that the way the systems works is to always give the answer that the teacher wants, no matter how uninspired!)
Next in the Richter series, we find eight puzzles similar to those in Fig. 12 except rectangular rather than square. These are shown in Fig. 14 without further comment, except to point out that puzzles with mostly dissimilar pieces are generally more interesting than those with many duplicates or triplicates.
Fig. 14
All of the Richter puzzles shown so far have used only 45-degree and 90-degree angles. Eight of the Richter puzzles are polygonal shapes dissected into pieces with 30-60-90-degree angles. These are shown in Fig. 15 arranged by increasing numbers of pieces.
Fig. 15
Most of the other Richter puzzles have curved outlines or other complications. For example, the two shown in Fig 16 have more complicated angles. In dissection puzzles of this type, if all of the angles and linear dimensions are not immediately obvious by inspection, then the design is probably not very well conceived.
Fig. 16
To digress slightly, a most curious dissection is the one shown in Fig. 17 on the left. This construction within a square appears in Curiosités Géométriques, by E. Fourrey, published in Paris in 1907. It is said to have been discovered in a 10th-century manuscript and is supposed to have been the work of Archimedes. At least three slightly different versions of it have appeared in modern puzzle books, all supposing it to be a geometrical dissection puzzle and calling it the "Loculus of Archimedes". One learns to be skeptical about such things, especially when they do not appear to make much sense and the original documents are reported lost. The mystery of its origin and its actual purpose is a challenging problem for recreational maths historians.
Fig. 17
It has been pointed out by some authors that the areas in the Loculus are cleverly devised to be in the ratios of whole numbers, as indicated. But there is nothing unusual about that. It is easily proven if not immediately obvious, that all polygons formed by connecting points on a regular square grid must have areas in the ratios of whole numbers. Less obvious but also provable is that polygons formed by intersections of such lines must also have this property, as in the example shown in Fig. 17 on the right. Exercise for the reader: compute the relative areas in this figure.
Note that none of the Richter puzzles has fewer than seven pieces, and several have more. One always tries to minimize the number of pieces without sacrificing other design objectives. Satisfactory dissection puzzles of this type with fewer than seven pieces are not as common, but possible. Consider the experience of another puzzle acquaintance of mine, Bill Trong. Bill made for himself a Tangram set from published plans, but he carelessly failed to make one cut, so he ended up with two of the pieces joined together and thus a set of six pieces. Surprisingly, he found he could construct all 13 of the convex patterns (Fig. 10) with this set. Which two pieces were joined together? Judge for yourself if this six-piece version is an improvement over the original Tangram.
Previously, the reader was asked if other convex Tangram solutions could be found. According to an article in American Mathematical Monthly, vol. 49, in 1942 Fu Traing Wang and Chuan-Chih Hsiung of the National University of Chekiang proved that no more than 13 different convex Tangrams can be formed. Their proof involved showing that there are only 20 possible ways of assembling the 16 unit triangles convexly, of which 13 were found to have Tangram solutions. An excellent discussion of this is given in Tangram, by Joost Elffers.
The point to be made here, before leaving the subject of Tangram, is that the simplest and most familiar puzzles often contain surprising recreational potential, much of which may have been overlooked. Some of the practical innovations may be quite clever too. Figure 18 shows an example of what one skilled and inspired woodcraftsman - Allan Boardman - has done with Tangram. The seven pieces fit with watchmaker's precision two layers deep into the tiny square box complete with sliding cover, all beautifully crafted of pearwood.
Fig. 18
| ©1990-2005 by Stewart T. Coffin For questions or comments regarding this site, contact the chief metagrobologist: |
[Next Page] [Prev Page] [ Next Chapter] [Prev Chapter]