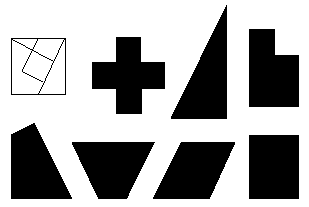
[Home] [Contents] [Figures] [Search] [Help]
[Next Page] [Prev Page] [ Next Chapter] [Prev Chapter]
Fig. 19 shows Sam Loyd's well known square-dissection puzzle. It is made by locating the midpoints of all four sides of the square, drawing the appropriate lines, and dissecting. The five pieces construct all of the puzzle patterns shown. Again note the interesting paradox of the two on the right - one being a solid rectangle and the other a rectangle with a corner missing, yet both use all five pieces.
Fig. 19
When one of Loyd's pieces is divided in two, the number of possible interesting puzzle patterns is approximately doubled. Some of these new patterns are shown in Fig. 20. The first problem for the reader is to discover the additional cut. It should be obvious which piece to divide. But which way?
Fig. 20
The reader is now encouraged to experiment with new and original dissection puzzles. Start with a simple shape such as a square or rectangle and dissect it according to some simple geometrical plan, the idea of which is to make pieces that fit together many different ways. Six or seven pieces is a good number. Try to avoid having many pieces alike, then create your own catalogue of pattern problems.
| ©1990-2005 by Stewart T. Coffin For questions or comments regarding this site, contact the chief metagrobologist: |
[Next Page] [Prev Page] [ Next Chapter] [Prev Chapter]