[Home] [Contents] [Figures] [Search] [Help]
[Next Page] [Prev Page] [ Next Chapter] [Prev Chapter]
At first glance, the nest of sticks shown in Fig. 93 may appear to be self-supporting. Any attempt to assemble it without tape or rubber bands will immediately dispel this notion as the sticks tumble into a heap. A useful tool for the puzzle designer would be some way of analyzing such geometrical arrangements to determine if they are interlocking or not, or even possible to assemble. If the arrangement is totally symmetrical, there is a simple way to do this, as follows:
To take a trivially simple example to start with, consider the Pin-Hole Puzzle without the pins and holes. In its assembled condition as shown (Fig. 94), the two ends of each piece rest flat against two others, and the ends of yet two others rest flat against it. Now move each piece by some incremental distance directly away from the center, and note that they become separated from each other. This is sufficient to show that the structure is non-interlocking and will easily fall apart.
Fig. 94
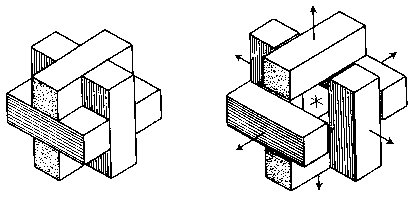
To take one more trivial example, consider a standard six-piece burr (Fig. 95) made up of six identical pieces like notchable piece no. 2 in Fig. 67. Applying this same test, we see that there is interference between the parts and therefore the burr is impossible to assemble.
Fig. 95
Now for a more practical example, consider the diagonal six-piece burr (Fig. 96). As each piece is moved an incremental distance away from the center, there is neither interference nor separation as the mating faces slide parallel to each other. Therefore it is an assemblable interlocking configuration.
Fig. 96
This useful theory of interlock can be applied most easily by using elementary vector analysis. If the radial movement of one piece is represented by vector A and that of a neighboring piece by vector B, then the relative motion of the two is vector A-B, and any sliding surface in an assemblable interlocking puzzle must be parallel to it. Or make a scale drawing of the puzzle and use methods of descriptive geometry. With a little practice and good spatial perception or a model to work with, most of the assemblies discussed in this book are easy to analyze. Applying this theory to the nest of 12 triangular sticks, it is easy to show that they are non-interlocking.
How might the 12 triangular sticks be made into an interlocking assembly? One way would be to use notched sticks, as in the burr puzzles. That scheme will be considered in Chapter 13. Another way is as follows, instead of leaving the center hollow, imagine it filled solid with a rhombic dodecahedron. Now dissect that rhombic dodecahedron into six identical blocks having the shape of squat octahedra, and use each one of them as a center block for joining the triangular sticks together in pairs, as shown in Fig. 97.
Fig. 97
If the theory of interlock is applied to this new six-piece puzzle configuration, it is found to be an interlocking assembly. It can be slid apart along any one of its four sliding axes, independently or concurrently. Unlike the diagonal burr, it separates into two halves that are quite dissimilar, even though each half is composed of three identical pieces and the completed assembly is symmetrical.
| ©1990-2005 by Stewart T. Coffin For questions or comments regarding this site, contact the chief metagrobologist: |
[Next Page] [Prev Page] [ Next Chapter] [Prev Chapter]