[Home] [Contents] [Figures] [Search] [Help]
[Next Page] [Prev Page] [ Next Chapter] [Prev Chapter]
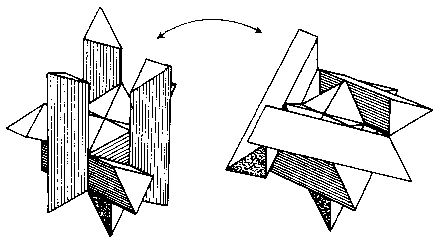
If both ends of all 12 sticks are now cut off at the appropriate angle (Fig. 98), an amazing transformation occurs and the assembly becomes the third stellation or the rhombic dodecahedron. (It is assumed that the reader has some familiarity with polyhedra and stellations. If not, any mathematics library should have a book on the subject.) Remove the equivalent of two tetrahedral blocks more from both ends of the sticks, and lo - the second stellation of the rhombic dodecahedron appears. Many intriguing intermediate forms are also possible by removing the equivalent of only one tetrahedral block, or by removing them selectively from certain ends. The biggest surprise occurs when yet two more tetrahedral units are removed from all the ends, producing the now familiar first stellation again (Fig. 99). Is this not amazing? It can be made not only from six square sticks with ends beveled but also from 12 triangular sticks!
Fig. 98
Fig. 99
| ©1990-2005 by Stewart T. Coffin For questions or comments regarding this site, contact the chief metagrobologist: |
[Next Page] [Prev Page] [ Next Chapter] [Prev Chapter]