[Home] [Contents] [Figures] [Search] [Help]
[Next Page] [Prev Page] [ Next Chapter] [Prev Chapter]
The Rosebud Puzzle consists of six pieces (Fig. 127a), of which three are identical and the other three are their reflexive pairs, except that one piece has a small hole for a removable pin. This puzzle has two symmetrical solutions, one of which (Fig. 127b) is decidedly more interesting than the other. Assembling it in the preferred solution requires the simultaneous manipulation of all six pieces in a manner that to begin with is not at all obvious and furthermore requires dexterity, patience, and some clever tricks.
Fig. 127a
Fig. 127b
A few of these puzzles were produced some years ago and sold unassembled. After sufficient time had elapsed and almost none had been solved, the customers were given the opportunity to purchase (for an outrageous price!) an assembly jig and directions. With these, it is easy. Without the jig, it can be done with patience, using tape and rubber bands. Without such aids, it has been done but borders on the impossible.
The reward for going to all this trouble is to discover the amazing mechanical action of the assembled puzzle. By placing three fingers of each hand in just the right places, it can be made to expand in a most fascinating manner, rather like the petals of a blooming flower (Fig. 127c). This effect is further enhanced by making the blocks of colorful woods with symmetrically matched grain. Then shift all six fingers slightly and the Rosebud closes again. By inserting the pin into the hole after assembly, one can play with the puzzle in this manner with no worry that it will fly apart.
Fig. 127c
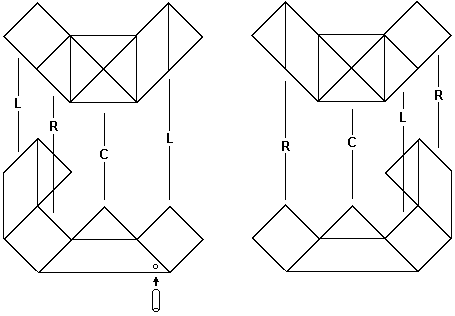
Standard building blocks are used in the construction of the puzzle pieces, as indicated. In order to be entirely satisfactory, they must be made very accurately with a smooth sliding action and must be strong.
The mechanical action of a coordinate-motion puzzle can be analyzed and explained using a vector diagram. For instance, in the first example shown, if the three rhombic blocks are A, B, and C, their relative motions are vectors AB, BC, and CA, which must form a closed loop and add up to zero - in this case by an equilateral triangle. The vector diagram of the Expanding Box Puzzle is an octahedron, and for the Rosebud Puzzle it is a triangular antiprism. The vector diagram for a coordinate-motion puzzle cannot be rectilinear. Why?
Although it is conceivable that one might design a coordinate-motion puzzle by studying vector diagrams, most such designs are just stumbled upon. The vector diagrams are presented here mostly as a curiosity.
| ©1990-2005 by Stewart T. Coffin For questions or comments regarding this site, contact the chief metagrobologist: |
[Next Page] [Prev Page] [ Next Chapter] [Prev Chapter]