[Home] [Contents] [Figures] [Search] [Help]
[Next Page] [Prev Page] [ Next Chapter] [Prev Chapter]
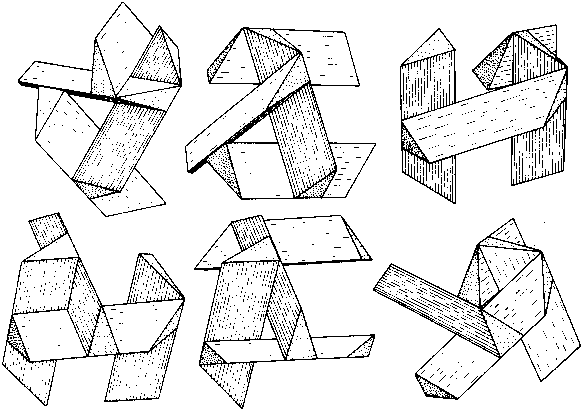
The 24 sticks in the Scorpius configuration lend themselves naturally to being joined in fours in different ways to create a combinatorial puzzle. Not counting side-by-side pairs, there are 10 different ways of joining four such sticks. Of these, one is symmetrical, two are impossible to assemble, and one does not permit any solutions. By a most extraordinary stroke of luck, the remaining six pieces, shown in Fig. 140a, assemble one way only with only one sliding axis and in essentially only one possible order to create a combinatorial puzzle of intriguing geometry and considerable difficulty. The Scrambled Scorpius in Fig. 140b was made by Mark McCallum.
Fig. 140a
Fig. 140b
For whatever it may be worth, the difficulty index of this puzzle is calculated as follows: the six pieces can be regarded as positioned roughly as the faces of a cube - top, bottom, front, back, left, right. Arbitrarily choose any piece for the bottom. Next, the piece on the left can be any one of the remaining five, oriented any one of four ways, and so on. So, 20 x 16 x 12 x 8 x 4 gives a difficulty index of 122,880 with just six simple pieces. Added to that is the amusement of figuring out the one correct order of assembly. All things considered, this is a most satisfactory puzzle and one that ought to be produced and enjoyed much more so than it has been. (Reference: US Patent Des. 230,288 to Coffin, 1974.)
| ©1990-2005 by Stewart T. Coffin For questions or comments regarding this site, contact the chief metagrobologist: |
[Next Page] [Prev Page] [ Next Chapter] [Prev Chapter]