[Home] [Contents] [Figures] [Search] [Help]
[Next Page] [Prev Page] [ Next Chapter] [Prev Chapter]
When dissected cubes are combined with whole cubes, the number of puzzling possibilities takes another quantum jump. This idea hatched just in time for inclusion in this book, so just one simple example will be given here.
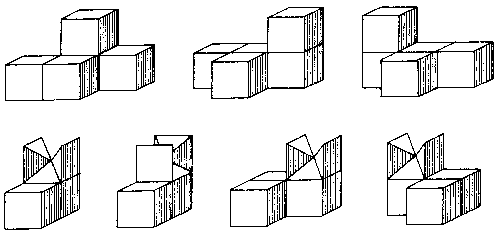
The set of seven dissimilar puzzle pieces shown in Fig. 184 could be described as three ordinary pentacube pieces and four jointed polycube half-pieces. They assemble one way only to form a 3 x 3 x 3 cube. The next time someone says that 3 x 3 x 3 cube puzzles are too easy, give them this one disassembled. Note that the half-pieces can be combined in pairs three different ways, with each pairing having four variations, so right there is ordinary puzzlement multiplied by a factor of 12!
Fig. 184
Now, if you are the type that likes to have a little extra fun sometimes, design a 3 x 3 x 3 cubic block puzzle like the above, except having only one jointed piece and with a tightly fitting joint. When carefully made these joints are practically impossible to detect. With the jointed piece assembled backwards, it looks like just an ordinary cubic block puzzle but is of course impossible to assemble.
With millions of possible combinations from which to choose, clever designs of this sort might incorporate many other interesting features such as interlocking assembly and construction of multiple symmetrical problem shapes. This leads into a whole new world of puzzling possibilities, almost totally unexplored, hence the name Pillars of Hercules. Note also that such puzzles are fairly easy to make in wood, since most of the blocks are just cubes. More intriguing still is the possibility of extending this idea to rhombic dodecahedra, with whole blocks and half-blocks combined, as suggested by the sample pieces shown in Fig. 185. Two of them form a small tetrahedron, three of them a triangle, and all five a large tetrahedron.
Fig. 185
| ©1990-2005 by Stewart T. Coffin For questions or comments regarding this site, contact the chief metagrobologist: |
[Next Page] [Prev Page] [ Next Chapter] [Prev Chapter]