[Home] [Contents] [Figures] [Search] [Help]
[Next Page] [Prev Page] [ Next Chapter] [Prev Chapter]
Although a well-crafted set of puzzle pieces for either of the two designs just described can be quite entertaining in itself, more important for the purpose of this book is that the geometrical principle they are both based on is even more fun to play with. It leads along an endless trail of new discoveries. For example, as suggested by Fig. 147, an obvious variation of the Six-Part Invention is to use the connection with three prongs rather than two. The three sample pieces shown in Fig. 180 assemble into a triangular cluster.
Fig. 180
By truncating the Eight-Piece Cube pieces to convert them into cuboctahedra, the puzzle remains the same but assumes an intriguing new geometry (Fig. 181).
Fig. 181
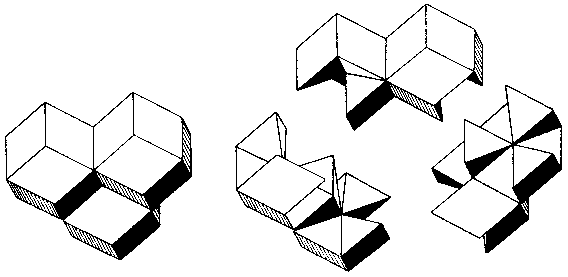
When any of the half-pieces described in this chapter are joined in threes rather than pairs, the numbers of puzzle pieces, practical sets, and possible constructions stretch the imagination. To give but one example, 12 identical pieces assemble to form the Triple Cross Puzzle shown in Fig. 182. Could you assemble 14 such pieces in axial symmetry? How about 46 such pieces?
Fig. 182
Now imagine combining all of the above into one super set containing singles, doubles, and triple pieces, and perhaps some even larger. Simply as a play construction set, who could possibly resist the urge to tinker with these pieces and fit them together different ways? At the same time, this versatile set of puzzle pieces contains practically unlimited potential as an educational tool and as a kit for discovering new puzzle problems, some of which should baffle experts. A few sample puzzle constructions are shown in Fig. 183. A large set of such pieces, well-crafted of hardwood, makes a marvelous construction set.
Fig. 183
| ©1990-2005 by Stewart T. Coffin For questions or comments regarding this site, contact the chief metagrobologist: |
[Next Page] [Prev Page] [ Next Chapter] [Prev Chapter]