[Home] [Contents] [Figures] [Search] [Help]
[Next Page] [Prev Page] [ Next Chapter] [Prev Chapter]
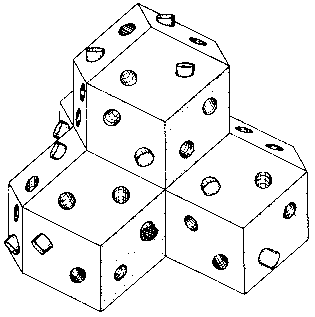
Carrying the scheme of the puzzle piece design shown in Fig. 200, to its obvious next step, make the rhombic dodecahedron itself the basic construction unit. Each block will have 12 holes. Four such blocks are shown in Fig. 201, assembled into a tetrahedral pile and pinned together by twelve dowels.
Fig. 201
In order to convert this intriguing construction set into an even more entertaining puzzle, we again join blocks and dowels to form lollipop pieces. But this time we also eliminate all extraneous holes. Not only does this save considerable drilling and improve the appearance, but it also adds greatly to the puzzling potential. By a judicious choice of hole locations, and stick locations in the lollipop pieces, simple constructions become fascinating puzzle problems. As a simple example, a triangular assembly of three blocks and three dowels is shown in Fig 202. Each block has two holes. Two pairs of blocks and dowels are joined to form lollipop pieces. The remaining dowel is the key.
Fig. 202
Note the similarities to the Pin-Hole Puzzle. The added feature of this new design is that even six or fewer rhombic dodecahedral blocks may be joined many different ways to create interesting geometrical shapes, as was shown for the Six-Part Invention in the preceding chapter. Thus, the natural appeal of pin-and-hole assembly pastimes is combined with the added feature of multiple assembly problems possible with one appropriately chosen set of puzzle pieces.
The arrangement of six blocks shown in Fig. 203 we have been calling an octahedral cluster. It uses 24 dowels. How many dowels may be attached to the blocks for it to still be assemblable? Can all the block pieces be dissimilar? What other puzzle problems can be devised using the same set of pieces? This should keep puzzle analysts busy for quite a while.
Fig. 203
There is a limit to the diameter of the dowels in relation to the blocks. The diagram in Fig. 204 shows the limit to be 1:6. In other words, if the blocks are 1½ inches across, the dowels cannot be more than ¼ inch diameter without interfering with each other.
Fig. 204
If the dowels are made slightly larger in diameter than the limit shown above, a most interesting puzzle results. Some of the dowels will require cylindrical notches milled into them. Twelve such dowels are shown in Fig. 205 assembled inside a rhombic dodecahedral block with 12 holes. Note the similarity to the 12 notched hexagonal sticks in Fig. 135a, but with some added mechanical constraints. Also, you cannot see what is going on inside. Here is a case where clear plastic might be used to advantage for the block, and perhaps even for the rods too. This puzzle scheme likewise offers recreation for the designer as well as the solver, since many different notch combinations are possible.
Fig. 205
| ©1990-2005 by Stewart T. Coffin For questions or comments regarding this site, contact the chief metagrobologist: |
[Next Page] [Prev Page] [ Next Chapter] [Prev Chapter]