Another common problem of complex search spaces is the existence of ridges. A ridge can be defined as a region of the search space where only a small fraction of the possible directions lead to a better value. How can a hill climber, with its limited number of steps, be sure that it has arrived at a peak and is not stuck on top of a ridge? This problem is common to any search algorithm that uses a fixed set of directions. This section will demonstrate how adapting step sizes provide an answer to this problem.
Figure 
illustrates the basic principle in two dimensions.
The concentric circles to the left of the figure are the contour map
of the objective function. It is a two-dimensional, unimodal
function. The maximum is at the center. The solid circle represents
the step size. The graph on the right shows the probability that a
random step will succeed in moving upward as a function of the ratio
of r1, which is the size of the step, to r2, the distance to the peak.
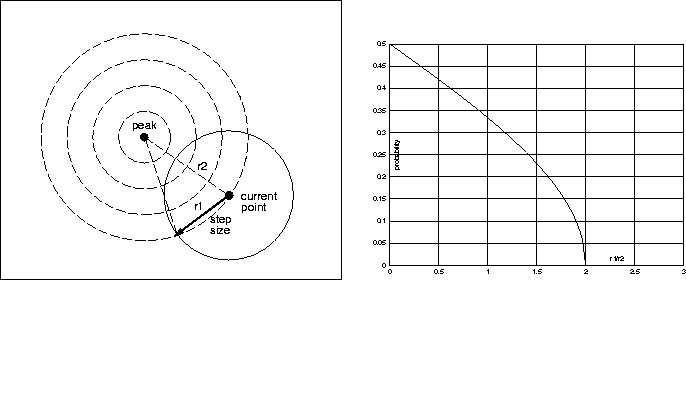
Figure:
The probability of success of a random step in two dimensions as a function of
the step size and the distance to the peak. Dashed circles are contour lines,
the solid circle is the potential points the step can take.
The important observation here is that the probability approaches 0.5 as the step size goes to 0. Intuitively, as the radius gets smaller, the iso-curve starts looking like a straight line (or a flat surface in higher dimensions) that cut our circle exactly in half. This is a general result that holds in any number of dimensions:
This assumes some smoothness in the objective function. Thus the choice of representation becomes important. There is a vast amount of work in genetic algorithms literature, on how to choose the right representations for certain problems. Every optimization algorithm has its ideal representation for a problem. The standard genetic algorithm favors the representations that make the problem separable, i.e. different parts of the solution can be discovered independently, and combined together. The method presented here, requires a representation in which one is able to use steps of various sizes. The larger step sizes should be more likely to bring about larger changes, and the small ones should locate the exact location of maxima. In most numerical problems this is natural. In combinatorial problems, one has to have a way to measure step size, even though the space is not Euclidean. I will present an example on the traveling salesman problem in the results chapter.
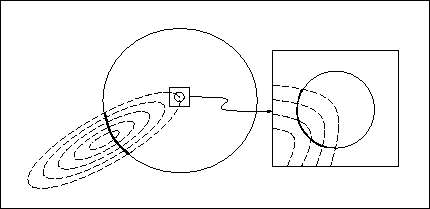
Figure:
How shrinking helps on ridges. The heavy arcs show the points that are better
than the current point. When the radius is smaller, as shown in the blow-up on
the right, this arc gets larger.
Figure shows how adapting step sizes can help the algorithm not
get stuck near ridges. This time the contours have the shape of narrow
ellipses. Thus a large step size has a low probability of success. However
after failing several times, the Local-Optimize
starts to shrink its
step size. The blow-up on the right shows how the picture looks when the step
size gets smaller. The sharp edges of the contours look flatter, so the arc of
points with better values than the current point, approaches a half circle.
Although shrinking down saves the algorithm from getting stuck, it also makes it slower. In search spaces where the direction of the ridge is changing, the local optimizer has to move with a lot of small zig-zags. However, augmenting it by adding by adding a small memory of recent moves that were successful, the performance increases dramatically. This is the topic of the next chapter.