The conformation of a molecule is a description of its 3-dimensional structure. The physical properties and biological functions of organic molecules are intimately related to their conformations. Thus computing energetically stable conformations of organic molecules is an important problem. One way to compute the conformations is to minimize an energy function, but unfortunately, the energy function typically has many local minima.
Figure:
The Cycloheptadecane molecule has 51 atoms. The three coordinates for each
atom are the input to the objective function. Thus the problem has 153
dimensions.
Procedure 2-1 was tried on a small instance of this problem. Cycloheptadecane
is a macrocyclic molecule. It consists of a chain of 17 carbons, where each
carbon is connected to two hydrogen atoms as well as two other neighbor
carbons. Figure 
illustrates this structure. There are a total
of 51 atoms in the molecule. Treating their x, y and z coordinates as separate
parameters of the energy function, we have an optimization problem of 153
dimensions.
Recently, a novel method to solve this problem efficiently was proposed
[Wang, 1994]. First, approximate solutions are found by combining smaller
chains together. Then, these approximate solutions are further refined in an
optimization loop. Figure contains the comparison of Procedure
2-1 with Powell's method in this loop as well as a sample run starting from a
random initial conformation.
Note that the gradient of the energy function typically can be computed. In that case an algorithm that can use this information such as conjugate gradient [Press et al., 1992,Polak, 1971], will be more efficient. The comparison is made with Powell's method because it is known as one of the most efficient algorithms among the ones that do not use the gradient.
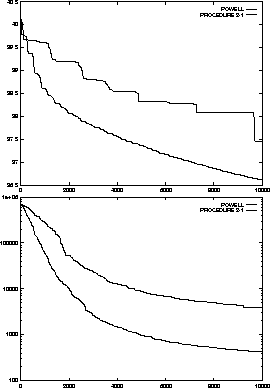
Figure:
Comparison of Procedure 2-1 with Powell's method on the molecule energy
minimization problem. The first example starts from a near optimal
configuration. The second example starts with a random configuration. The
lower lines are the traces of Procedure 2-1.