The traveling salesman problem is the problem of finding the shortest cyclical itinerary for a traveling salesman who must visit each of N cities in turn. This problem has a very different nature from the above problems, it is an example of combinatorial optimization. There is an objective function to be minimized, but the search space is the discrete space of all permutations of N cities. The combinatorial optimization problems are challenging because the number of elements in the search space is factorially large, thus they cannot be exhaustively searched. Also it is hard to define a concept of ``direction'' in a permutation space.
The representation one chooses to use might make it possible to define concepts of ``distance'' and ``direction'' in non-cartesian spaces. One can carefully define various mutations such that ``moving further in the same direction'' is meaningful. It is also possible to define a notion of ``size'' in carefully selected operations. I will not present a detailed study of the application of my program on combinatorial problems. However, I thought it desirable to include one example, to show that the same key ideas apply even when one does not have a cartesian space.
I compared the results I obtained from a very simple implementation of my algorithm with results from simulated annealing. The simulated annealing program [Press et al., 1992] uses an efficient set of moves suggested by Lin [Lin, 1965]. The moves consist of two types: (a) A section of path is removed and then replaced with the same cities running in the opposite order; or (b) a section of path is removed and then replaced in between two cities on another, randomly chosen, part of the path. The objective function is the total length of the journey.
The implementation of Procedure 2-1 only uses the first type move, i.e. reversing a section of the path. The size of a step is defined as the width of the section reversed. The same principles of adjusting the step size are used.
Although this is a very different problem, the results of Procedure 2-1 are
comparable to that of simulated annealing. Figure 
shows the
average over 10 runs for problems of 10 randomly selected city coordinates.
These demonstrate that the main ideas presented in this thesis are not specific
to numerical problems, but are general principles useful for optimization in
general.
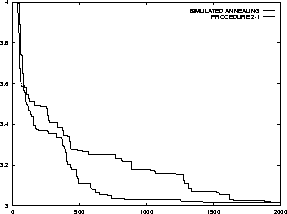
Figure:
The performance of my algorithm compared to simulated annealing on the
traveling salesman problem averaged over ten runs. The x axis shows the number
of operations tried and the y axis shows the distance of the best discovered
path.