Introduction

In this chapter I define the problem of optimization, explain the problems usually associated with optimization, establish criteria for success for optimization algorithms, and introduce several key heuristic ideas.

The goal of optimization is, given a system, to find the setting of its parameters that yields optimal performance. The performance measure is given as an objective function.

The cases where the parameter space can be searched exhaustively or the objective function can be subjected to analytical methods are not considered in this thesis. Thus, it is assumed that the only source of information available to an optimization algorithm is the evaluation of the objective function at a limited number of selected points as in Figure .

What makes global optimization a challenging problem are the potential existence of many local maxima, a high number of dimensions, uncooperative twists and turns in the search space, and an objective function that is costly to compute. For a general introduction to computational methods in optimization see [Polak, 1971], or [Dennis and Schnabel, 1983].

  
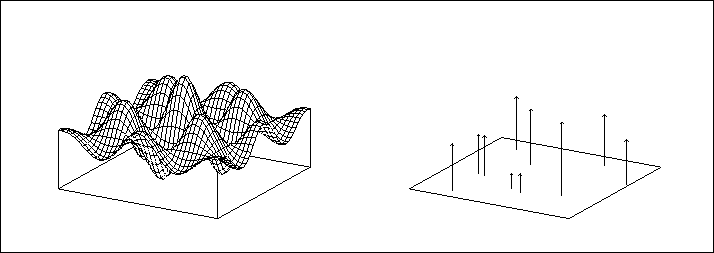
Figure: The first figure shows a typical objective function. The second shows the information available to the optimization algorithm.

The work described in this thesis started with explorations with genetic-algorithms. Typical programs based on the genetic-algorithm idea suffer not only from all of the problems that generally plague attempts at global optimization, but also from problems that are specific to the use of populations subject to survival pressures.

In particular, local optima attract populations like magnets. The right way to maintain diversity is not clear. Most proposed solutions end up modifying the objective function, which can result in the total loss of the global optimum [Winston, 1992], or are specific to the particular problem at hand and difficult to generalize [Hillis, 1990].

Also, the large number of individuals involved in the typical genetic program results in a large number of function evaluations. Especially in problems with a high number of parameters, this considerably slows the genetic algorithm down.

The search for a systematic approach to these problems and experiments with numerous algorithms [Yuret, 1992,Yuret and de la Maza, 1993,de la Maza and Yuret, 1994] finally led to the following three key heuristics:

• Remember the locations of local maxima and restart the optimization program at a place distant from previously located local maxima.
• Adjust the size of probing steps to suit the local nature of the terrain, shrinking when probes do poorly and growing when probes do well.
• Keep track of the directions of recent successes, so as to probe preferentially in the direction of most rapid ascent.

None of these three heuristics is new, and none of them are specific to optimization. Nevertheless, the combination leads to a powerful optimization method. The generality of the ideas ensures the algorithm's adaptability to a wide range of problems. This is justified by the empirical evidence on several real-world problems, where the method outperformed well established algorithms such as Powell's method and simulated annealing.

The next three chapters take each of these key ideas in turn, and analyze their contribution to the overall picture. This is followed by test results and analysis of related work on several problems. The last chapter concludes with a summary of the thesis and discussion of future work. Sample code is provided in the appendix.