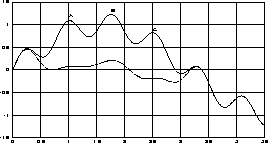
Figure: The discovery of the local maxima at A and C result in a modification of the objective function such that the global maximum at B is no longer visible.




Local maxima are a major problem not just for genetic algorithms, but any optimization technique that sets out to find the global optimum. A genetic algorithm works nicely in the exploration stage, with each of the individuals discovering pieces of the solution and combining them together. However when a locally optimal point is achieved by a particular individual, it manages to hold the lead for a number of iterations and all individuals start looking alike. The leader survives through generations, and contributes in many crossovers, distributing its genes to every other candidate. The distant explorers are outperformed and gradually eliminated. Finally, progress comes to a halt when diversity ceases to exist.

Figure:
The discovery of the local maxima at A and C result in a modification of
the objective function such that the global maximum at B is no longer visible.
The initial approach taken for this research was making diversity a part of the
fitness function [Winston, 1992,Yuret, 1992]. This works by populating the local
maxima in order to avoid them. When diversity is part of the fitness function,
the individuals that are close to an already populated local maxima are
punished, and distant explorers are rewarded. There are several difficulties
with this approach. First, it is not clear how to combine fitness with
diversity, and experiments [Yuret, 1992] suggest that an implementation
good for one particular problem has difficulty with another. Second, as the
number of discovered local maxima increases, the size of the population has to
increase also. Otherwise the population ``forgets'' some of the local maxima
and new generations keep falling into the old traps. Finally, as with any
method that permanently modifies the objective function, there is the danger of
covering the actual global optimum, and making it impossible to find. An
example is given in Figure  . An optimization algorithm should
never lose the possibility of finding the global optimum.
. An optimization algorithm should
never lose the possibility of finding the global optimum.
The problem of forgetting the local maxima is particularly interesting. It suggests a dynamic population size that grows as more local maxima are discovered. However, this will reduce efficiency because simulating each generation will become more expensive. The next section presents a way to get around this problem. The section after next will illustrate how to use local maxima without modifying the evaluation function.



