3. Lexical Attraction Models

A probabilistic language model is a representation of linguistic knowledge which assigns a probability distribution over the possible strings of the language. This chapter presents a new class of language models called lexical attraction models. Within the framework of lexical attraction models it is possible to represent syntactic relations which form the basis for extraction of meaning. Syntactic relations are defined as pairwise relations between words identifiable in the surface form of the sentence. Lexical attraction is formalized as the mutual information captured in a syntactic relation. The set of syntactic relations in a sentence is represented as an undirected, acyclic, and planar graph^3.1. I show that the entropy of a lexical attraction model is determined by the mutual information captured in the syntactic relations given by the model. This is a prelude to the central idea of the next chapter: The search for a low entropy language model leads to the unsupervised discovery of syntactic relations.

3.1 Syntactic relations are primitives of language

A defining property of human language is compositionality, i.e. the ability to construct compound meanings by combining simpler ones. The meaning of the sentence ``John kissed Mary'' is more than just a list of the three concepts John, kiss, and Mary. Part of the meaning is captured in the way these concepts are brought together, as can be seen by combining them in a different way: ``Mary kissed John'' has a different meaning.

Language gives us the ability to describe concepts in certain semantic relations by placing the corresponding words in certain syntactic positions. However, all languages are restricted to using a small number of function words, affixes, and word order for the expression of different relations because of the one dimensional nature of language. Therefore, the number of different syntactic arrangements is limited. I define the set of relations between words identifiable in the syntactic domain as syntactic relations. Examples of syntactic relations are the subject-verb relation, the verb-object relation and prepositional attachments.

Because of the limited number of possible syntactic relations there is a many to one mapping from conceptual relations to syntactic relations. Compare the sentences ``I saw the book'' and ``I burnt the book''. The conceptual relation between see and book is very different from the one between burn and book. For the verb see, the action has no effect on the object, whereas for burn it does. Nevertheless they have to be expressed using the same verb-object relation. The different types of syntactic relations constrain what can be expressed and distinguished in language. Therefore, I take syntactic relations as the representational primitives of language.

A phrase-structure representation of a sentence reveals which words or phrases combine to form higher order units. The actual syntactic relations between words are only implicit in these groupings. In a phrase-structure formalism, the fact that John is the subject of kissed can only be expressed by saying something like ``John is the head of a noun-phrase which is a direct constituent of a sentence which has a verb-phrase headed by the verb kissed.''

I chose to use syntactic relations as representational primitives for two reasons. First, the indirect representation of phrase-structure makes unsupervised language acquisition very difficult. Second, if the eventual goal is to extract meaning, then syntactic relations are what we need, and phrase-structure only indirectly helps us retrieve them. Instead of assuming that syntactic relations are an indirect by-product of phrase-structure, I chose to take syntactic relations as the basic primitives, and treat phrase-structure as an epiphenomenon caused by trying to express syntactic relations within the one dimensional nature of language.

The linguistic formalism that takes syntactic relations between words as basic primitives is known as the dependency formalism. Mel'cuk discusses important properties of syntactic relations in his book on dependency formalism [Mel'cuk, 1988]. A large scale implementation of English syntax based on a similar formalism by Sleator and Temperley uses 107 different types of syntactic relations such as subject-verb, verb-object, and determiner-noun [Sleator and Temperley, 1991].

I did not differentiate between different types of syntactic relations in this work. The goal of the learning program described in Chapter 4 is to correctly determine whether or not two words in a sentence are syntactically related. Learning to differentiate between different types of syntactic relations in an unsupervised manner is discussed in that chapter.

3.2 Lexical attraction is the likelihood of a syntactic relation

In order to understand a sentence, one needs to identify which words in the sentence are syntactically related. Lexical attraction is the likelihood of a syntactic relation. In this section I formalize lexical attraction within the framework of information theory.

Shannon defines the entropy of a discrete random variable as $H = -\sum p_i \log p_i$ where i ranges over the possible values of the random variable and p_i is the probability of value i[Shannon, 1948,Cover and Thomas, 1991]. Consider a sequence of tokens drawn independently from a discrete distribution. In order to construct the shortest description of this sequence, each token i must be encoded using $-\log_2 p_i$ bits on average. $-\log_2 p_i$ can be defined as the information content of token i. Entropy can then be interpreted as the average information per token. Following is an English sentence with the information content of each word^3.2 given below, assuming words are independently selected. Note that the information content is lower for the more frequently occurring words.

(4)  

Why do we care about encoding or compression? The total information in sentence (4) is the sum of the information of each word, which is 99.28 bits. This is mathematically equivalent to the statement that the probability of seeing this sentence is the product of the probabilities of seeing each word, which is 2^-99.28. Therefore there is an equivalence between the entropy and the probability assigned to the input. A probabilistic language model assigns a probability distribution over all possible sentences of the language. The maximum likelihood principle states that the parameters of a model should be estimated so as to maximize the probability assigned to the observed data. This means that the most likely language model is also the one that achieves the lowest entropy.

A model can achieve lower entropy only by taking into account the relations between the words in the sentence. Consider the phrase Northern Ireland. Even though the independent probability of Northern is 2^-12.6, it is seen before Ireland 36% of the time. Another way of saying this is that although Northern carries 12.6 bits of information by itself, it adds only 1.48 bits of new information to Ireland.

With this dependency, Northern and Ireland can be encoded using 1.48+14.65=16.13 bits instead of 12.60+14.65=27.25bits. The 11.12 bit gain from the correlation of these two words is called mutual information. Lexical attraction is measured with mutual information. The basic assumption of this work is that words with high lexical attraction are likely to be syntactically related.

3.3 The context of a word is given by its syntactic relations

The Northern Ireland example shows that the information content of a word depends on other related words, i.e. its context. The context of a word in turn is determined by the language model used. In this section, I describe a new class of language models called lexical attraction models. Within the lexical attraction framework, it is possible to represent a linguistically plausible context for a word.

The choice of context by a language model implies certain probabilistic independence assumptions. For example, an n-gram model defines the context of a word as the n-1 words immediately preceding it. Diagram (5) gives the information content of the words in (4) according to a bigram model. The arrows show the dependencies. The information content of Northern and Ireland is different from the previous section because of the different dependencies. The assumption is that each word is conditionally independent of everything but the adjacent words. The information content of each word is computed based on its conditional probability given the previous word. As a result, the encoding of the sentence is reduced from 99.28 bits to 62.34 bits.

(5)  

Two words in a sentence are almost never completely independent. In fact, Beeferman et al. report that words can continue to show selectional influence for a window of several hundred words [Beeferman et al., 1997]. However, the degree of the dependency falls exponentially with distance. That justifies the choice of the n-gram models to relate dependency to proximity.

Nevertheless, using the previous n-1 words as context is against our linguistic intuition. In a sentence like ``The man with the dog spoke'', the selection of spoke is influenced by man and is independent of the previous word dog. It follows that the context of a word would be better determined by its linguistic relations rather than according to a fixed pattern.

Words in direct syntactic relation have strong dependencies. Chomsky defines such dependencies as selectional relations [Chomsky, 1965]. Subject and verb, for example, have a selectional relation, and so do verb and object. Subject and object, on the other hand, are assumed to be chosen independently of one another. It should be noted that this independence is only an approximation. The sentences ``The doctor examined the patient'' and ``The lawyer examined the witness'' show that the subject can have a strong influence on the choice of the object. Such second degree effects are discussed in Chapter 4.

The following diagram gives the information content of the words in sentence (4) based on direct syntactic relations:

(6)  

The arrows represent the head-modifier relations between words. The information content of each word is computed based on its conditional probability given its head. I marked the verb as governing the auxiliary and the noun governing the preposition which may look controversial to linguists. From an information theory perspective, the mutual information between content words is higher than that of function words. Therefore my model does not favor function word heads.

The probabilities were estimated by counting the occurrences of each pair in the same relative position. The linguistic dependencies reduce the encoding of the words in this sentence to 49.85 bits compared to the 62.34 bits of the bigram model^3.3.

Every model has to make certain independence assumptions, otherwise the number of parameters would be prohibitively large to learn. The choice of the independence assumptions determine the context of a word. The assumption in (6) is that each word depends on one other word in the sentence, but not necessarily an adjacent word as in n-gram models. I define the class of language models that are based on this assumption as lexical attraction models. Lexical attraction models make it possible to define the context of the word in terms of its syntactic relations.

3.4 Entropy is determined by syntactic relations

I define the set of probabilistic dependencies imposed by syntactic relations in a sentence as the dependency structure of the sentence. The strength of the links in a dependency structure is determined by lexical attraction. In this section I formalize dependency structures as Markov networks and show that the entropy of a language model is determined by the mutual information captured in syntactic relations.

A Markov network is an undirected graph representing the joint probability distribution for a set of variables^3.4 [Pearl, 1988]. Each vertex corresponds to a random variable, a word in our case. The structure of the graph represents a set of conditional independence properties of the distribution: each variable is probabilistically independent of its non-neighbors in the graph given the state of its neighbors.

You can see two interesting properties of the dependency structure in diagram (6): The graph formed by the syntactic relations is acyclic and the links connecting the words do not cross. In this section you will also see that the directions of the links do not effect the joint probability of the sentence, thus the links can be undirected. I discuss these three properties below and derive a formula for the entropy of the model.

Dependency structure is acyclic

The syntactic relations in a sentence form a tree. Trees are acyclic. Linguistically, each word in a sentence has a unique governor, except for the head word, which governs the whole sentence^3.5. If you assume that each word probabilistically depends on its governor, the resulting dependency structure will be a rooted tree as in diagram (6).

Dependency structure is planar

Most sentences in natural languages have the property that syntactic relation links drawn over words do not cross. This property is called planarity [Sleator and Temperley, 1993], projectivity [Mel'cuk, 1988], or adjacency [Hudson, 1984] by various researchers. The examples below illustrate the planarity of English. In sentence (7), it is easily seen that the woman was in the red dress and the meeting was in the afternoon. However, in sentence (8) the same interpretation is not possible. In fact, it seems more plausible for John to be in the red dress.

(7)  

(8)  

Gaifman gave the first formal analysis of dependency structures that satisfy the planarity condition[Gaifman, 1965]. His paper gives a natural correspondence between dependency systems and phrase-structure systems and shows that the dependency model characterized by planarity is context-free. Sleator and Temperley show that their planar model is also context-free even though it allows cycles [Sleator and Temperley, 1991].

Lexical attraction is symmetric

Lexical attraction between two words is symmetric. The mutual information is the same no matter which direction the dependency goes. This directly follows from Bayes' rule. What is less obvious is that the choice of the head word and the corresponding dependency directions it imposes do not effect the joint probability of the sentence. The joint probability is determined only by the choice of the pairs of words to be linked. Therefore dependency structures can be formalized as Markov networks, i.e. they are undirected.

Consider the Northern Ireland example:

(9)

In the first case, I used the conditional probability of Northern given that the next word is Ireland. In the second case, I used the conditional probability of Ireland given that the previous word is Northern. In both cases the encoding of the two words is 16.13 bits, which is in fact $-\log_2 p$ of the joint probability of Northern Ireland. Thus a more natural representation would be (10), where the link has no direction and its label shows the number of bits gained, mutual information:

(10)  

I generalize this result below and use the same representation for the whole sentence:

(11)  

Theorem 1   The probability of a sentence with a given dependency structure does not depend on the choice of the head word.

Proof: Consider a sentence S where:

$$\begin{eqnarray*}W &=& \{w_0, w_1, \ldots, w_n\} \\ L &=& \{(w_{i1},w_{j1}), (w_{i2},w_{j2}), \ldots\} \end{eqnarray*}$$

denote words and links respectively. Let P(L) denote the probability of a sentence having the dependency structure given by L. Assume that w₀ is the head word and every word probabilistically depends only on its governor. Then the joint probability of the sentence is given by the following expression:

(12)  $\parbox{3in}{ \begin{eqnarray*} P(S) & = & P(L) P(w_0) \prod_{(w_i,w... ...P(w_i) \prod_{(w_i,w_j)\in L} \frac{P(w_i,w_j)}{P(w_i) P(w_j)} \end{eqnarray*}}$

In the final expression P(w₀) plays no special role, i.e. starting from any other head word, I would have arrived at the same result. Therefore the choice of the head and the corresponding directions imposed on the links are immaterial for the probability of the sentence.

Encoding of dependency structure is linear

The P(L) factor in (12) represents the prior probability that the language model assigns to a dependency structure. In n-gram models P(L) is always 1, because there is only one possible dependency structure. In probabilistic context free grammars, the probabilities assigned to grammar rules impose a probability distribution over possible parse trees. In my model, I assume a uniform distribution over all possible dependency structures, i.e. P(L) = 1/|L|, where |L| is the number of possible dependency structures.

Without the planarity condition, the number of possible dependency structures for an n word sentence would be given by Cayley's formula: n^n-2 [Harary, 1969]. The encoding of the dependency structure would then take $O(n\log n)$ bits. However, the encoding of planar dependency structures is linear in the number of words as the following theorem shows.

Theorem 2   Let f(n) be the number of possible dependency structures for an n+1 word sentence. We have:

$$f(n) = \frac{1}{2n+1} \left(\begin{array}{c}3n\\ n\end{array}\right)$$

Proof: Consider a sentence with n+1 words as in (13). The leftmost word w₀ must be connected to the rest of the sentence via one or more links. Even though the links are undirected, I will impose a direction taking w₀ as the head to make the argument simpler. Let w_i be the leftmost child of w₀. We can split the rest of the sentence into three groups: Left descendants of w_i span w₁^i-1, right descendants of w_i span w_i+1^j, and the rest of the sentence spans w_j+1ⁿ. Each of these three groups can be empty. The notation w_i^j denotes the span of words $w_i \ldots w_j$.

(13)  

The problem of counting the number of dependency structures for the n words headed by w₀ can be split into three smaller versions of the same problem: count the number of structures for w₁^i-1headed by w_i, w_i+1^j headed by w_i, and w_j+1ⁿ headed by w₀. Therefore f(n) can be decomposed with the following recurrence relation:

$$f(n) = \sum_{p+q+r=n-1} f(p) f(q) f(r) \mbox{\hspace{1cm}} p,q,r \ge 0$$

Here the numbers p, q, and r represent the number of words in w₁^i-1, w_i+1^j, and w_j+1ⁿ respectively. This is a recurrence with 3-fold convolution. The general expression for a recurrence with m-fold convolution is C(mn,n)/(mn-n+1) where C is the binomial coefficient [Graham et al., 1994, p. 361]. Therefore f(n) = C(3n,n)/(2n+1).

The first few values of f(n) are: 1, 1, 3, 12, 55, 273, 1428. Figure 3.1 shows the possible dependency structures with up to four words.

  

Figure 3.1: Possible dependency structures with up to four words

An upper bound on the number of dependency structures can be obtained using the following inequality given in [Cormen et al., 1990, p. 102]:

$$\begin{eqnarray*}\left(\begin{array}{c}n\\ k\end{array}\right) & \le & \frac{n^n... ...ac{(3n)^{3n}}{(n)^{n} (2n)^{2n}} \\ & = & \frac{3^{3n}}{2^{2n}} \end{eqnarray*}$$

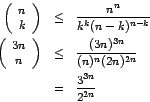
Taking the logarithm of this value and dividing it by n, you can see that the encoding of a planar dependency structure takes less than $3\log_2 3 - 2 \approx 2.75$ bits per word.

Entropy is determined by syntactic relations

With these results at hand, it is revealing to look at (12) from an information theory perspective. The final expression of (12) can be rewritten as:

$$-\log_2 P(S) = - \sum_{w_i\in W} \log_2 P(w_i) - \log_2 P(L) - \sum_{(w_i,w_j)\in L} \frac{P(w_i,w_j)}{P(w_i) P(w_j)}$$

This can be interpreted as:

(14)   information in a sentence = information in the words
+ information in the dependency structure
- mutual information captured in syntactic relations.

The average information of an isolated word is independent of the language model. I also showed that the encoding of the dependency structure is linear in the number of words for lexical attraction models. Therefore the first two terms in (14) have a constant contribution per word and the entropy of the model is completely determined by the mutual information captured in syntactic relations.

3.5 Summary

Part of the meaning in language is captured in the way words are arranged in a sentence. This arrangement implies certain syntactic relations between words. With a view towards extraction of meaning, I adopted a linguistic representation that takes syntactic relations as its basic primitives.

I defined lexical attraction as the likelihood of two words being related. The language model determines which words are related in a sentence. For example, n-gram models assume that each word depends on the previous n-1 words. I defined a new class of language models called lexical attraction models where each word depends on one other word in the sentence which is not necessarily adjacent, provided that link crossing and cycles are not allowed. It is possible to represent linguistically plausible head modifier relationships within this framework. I showed that the entropy of such a model is determined by the lexical attraction between related words.

The examples in this chapter showed that using linguistic relations between words can lead to lower entropy. Conversely, the search for a low entropy language model can lead to the unsupervised discovery of linguistic relations, as I will show in the next chapter.